Der Schwerpunkt (Baryzentrum) ![]() eines Polygons berechnet sich als
baryzentrische Kombination aus den Eckpunkten
eines Polygons berechnet sich als
baryzentrische Kombination aus den Eckpunkten ![]() des Polygons,
versehen mit Gewichten
des Polygons,
versehen mit Gewichten ![]() :
:
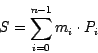
Für ein Dreieck gilt z.B.:
Und für ein Viereck gilt:
Bei baryzentrischen Kombinationen von Punkten gilt immer:
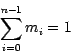
Die ![]() sind im Allgemeinen verschieden und repräsentieren in der Physik
die Massen der beteiligten Massenpunkte
sind im Allgemeinen verschieden und repräsentieren in der Physik
die Massen der beteiligten Massenpunkte ![]() .
.
Baryzentrische Kombinationen sind die einzige Möglichkeit Punkte sinnvoll additiv miteinander zu verknüpfen.