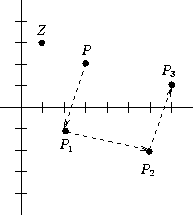Weder ![]() noch
noch ![]() dürfen gleich
dürfen gleich ![]() sein. Sonst würde das 2D-Objekt
in einer Dimension (oder gar beiden Dimensionen) auf die Ausdehnung
sein. Sonst würde das 2D-Objekt
in einer Dimension (oder gar beiden Dimensionen) auf die Ausdehnung ![]() zusammengestaucht. Die Objekte sind aber zweidimensional und sollen es im
Laufe der Transformationen auch bleiben.
zusammengestaucht. Die Objekte sind aber zweidimensional und sollen es im
Laufe der Transformationen auch bleiben.
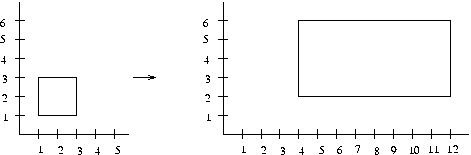
Abbildung
6.2
zeigt ein
Beispiel für eine Skalierung bezüglich
des Ursprungs mit den Faktoren ![]() ,
, ![]() .
.
Bei Wahl eines beliebigen Fixpunktes
![]() folgt für
den Punkt
folgt für
den Punkt ![]() :
:
Die neuen Koordiaten berechnen sich dann wie folgt:
Vorteilhafter bei mehreren Objekten:
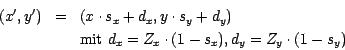
Abbildung
6.3
zeigt ein
Beispiel für eine Skalierung bezüglich
des Punktes ![]() mit den Faktoren
mit den Faktoren ![]() ,
, ![]() .
.