| Regelmenge |
|
||
|
|
|||
|
|
|||
|
|
Ausgehend von einem Startwort ![]() wird in jedem
Iterationsschritt auf jedes Zeichen von
wird in jedem
Iterationsschritt auf jedes Zeichen von ![]() eine Regel aus
eine Regel aus ![]() angewandt.
angewandt.
Sei ![]() . Dann ist
. Dann ist
![]() .
.
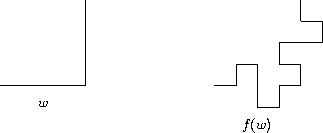
Ist nach ![]() Iterationen das Wort
Iterationen das Wort ![]() entstanden,
so kann es, zusammen mit dem Parameter
entstanden,
so kann es, zusammen mit dem Parameter ![]() (erforderlich für die
Schrittweite), einer Ausgabeprozedur übergeben werden.
(erforderlich für die
Schrittweite), einer Ausgabeprozedur übergeben werden.
Die quadratische Koch-Kurve hat die Dimension
![]() , denn jeder Kantenzug besteht
aus
, denn jeder Kantenzug besteht
aus ![]() Kopien, jeweils skaliert um den Faktor
Kopien, jeweils skaliert um den Faktor
![]() .
.
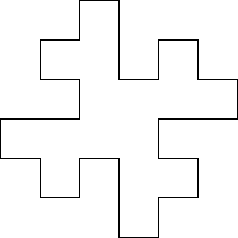
|

|