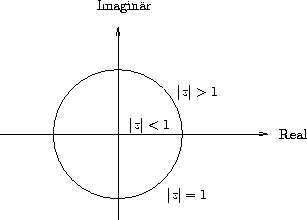
Es gilt: Julia-Menge für ![]() ist genau dann zusammenhängend, wenn
ist genau dann zusammenhängend, wenn ![]() in der Mandelbrotmenge
für
in der Mandelbrotmenge
für ![]() liegt.
liegt.
|

|
Implementation der Julia-Menge:
void julia_voll( // berechnet Julia-Menge als gefuelltes Gebiet
Complex c, // fuer komplexes c,
Complex start, // die linke obere Ecke start der komplexen Flaeche,
double schritt, // Schrittweite schritt
int max_iter) // mit vorgegebener Iterationszahl max_iter
{
Point p = new Point();
Point q = new Point(); // Symmetrischer Punkt
int zaehler ;
Complex z;
for (p.x = 0; p.x <= WIDTH; p.x++)
for (p.y = 0; p.y <= HEIGHT/2; p.y++)
// Wegen Symmetrie nur bis zur Haelfte laufen
{
z = new Complex(p, start, schritt);
q.x = WIDTH - p.x; // Symmetrie nutzen
q.y = HEIGHT - p.y;
zaehler = 0;
while ((q_betrag(z) < 4.0) && (zaehler++ < max_iter))
{
z = f(z,c);
}
if (q_betrag(z) < 4.0)
{
set_pixel(p);
set_pixel(q);
}
}
}
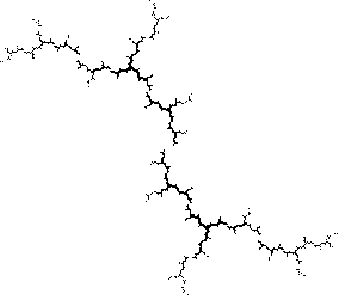
Es gilt: Der Rand der berechneten Fläche stellt die Julia-Menge
für ![]() dar.
dar.
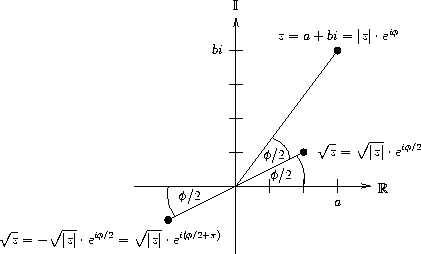
Sei ![]() eine komplexe Zahl.
Es gilt:
eine komplexe Zahl.
Es gilt:
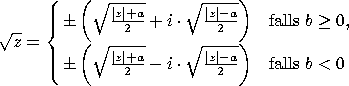
Realisiere ![]() durch
durch
Complex backward_random (Complex z, Complex c)
{
/* z = z - c */
/* bestimme r mit r * r = z */
/* wuerfel das Vorzeichen von r */
return (r);
}
Die Wahl des Vorzeichens bei dieser inversen Iteration erfolgt zufällig.
Ausgehend von ![]() werden zunächst 50 Iterationen
werden zunächst 50 Iterationen ![]() durchgeführt,
um die berechneten Punkte nahe genug an die Julia-Kurve heranzuführen.
Iteriere danach weiter
durchgeführt,
um die berechneten Punkte nahe genug an die Julia-Kurve heranzuführen.
Iteriere danach weiter ![]() und zeige jeweils die berechneten
und zeige jeweils die berechneten ![]() :
:
void julia_rueck( // berechnet Julia-Menge
Complex c, // fuer komplexes c
Complex start, // linke obere Ecke der komplexen Flaeche
double schritt, // Schrittweite
int anzahl) // durch anzahl Rueckwaertsspruenge
{
int k;
Complex z = new Complex(1.0, 0.0); // Startposition
for (k=0; k<50; k++) // tastet sich an die Julia-Kurve heran
z = backward_random(z,c);
for (k=0; k < anzahl; k++) { // bestimme anzahl Vorgaenger
z = backward_random(z,c);
set_pixel(z.getPoint(start, schritt)); // und zeichne sie
}
}