Iterierte Funktionensysteme

Iterierte Funktionssysteme sind in der Lage, mit wenigen Regeln komplexe, natürlich aussehende Bilder zu erzeugen. Hierbei wird eine Folge von Punkten im $\mathbf{R}^2$ durch fortgesetzte Anwendung von affinen Transformationen durchlaufen. Jede Transformation ist definiert durch eine $2\times 2$- Deformationsmatrix $A$, einen Translationsvektor $b$ und eine Anwendungswahrscheinlichkeit $w$, wodurch ein Punkt $\overline{x}$ abgebildet wird auf $A \overline{x} + b$. Zum Beispiel erzeugen folgende 4 Regeln das Farnblatt in Abbildung 11.13 :

Abbildung 11.13: Vom Iterierten-Funktionen-System erzeugter Farn

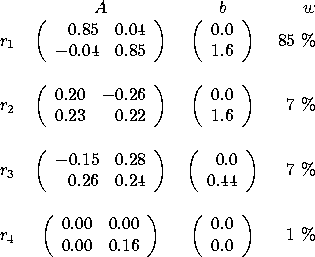
Eine alternative Sichtweise zur Definition eines fraktalen Bildes verlangt die Selbstähnlichkeit von Teilen des Bildes mit dem Ganzen.

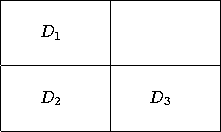
Beispielsweise sei ein Rechteck $R$ gesucht, so daß sich sein Inhalt, jeweils auf ein Viertel verkleinert, im linken oberen, linken unteren und rechten unteren Quadranten wiederfindet. Beginnend mit einem beliebigen Rechteckinhalt werden die 3 Quadranten so lange als skalierte Versionen des Gesamtrechtecks ersetzt, bis wir nahe am Fixpunkt dieser Iterationen angelangt sind. Das Ergebnis ist das sogenannte Sierpinsky-Dreieck.

Abbildung 11.14: Sierpinsky-Dreieck