


Previous: Analyse der Laufzeit der linearen Suche
Up: Lineare und binäre Suche
Next: Klassenmethoden
- Beh.:
- In einem Schleifendurchlauf schrumpft ein Intervall der Länge
2k - 1 auf ein Intervall der Länge
2k - 1 - 1 .
Beweis:
Sei Länge vom alten Intervall =
| |
2k - 1 |
= |
 - -  + 1 + 1 |
|
|
 |
2k |
= |
 - - 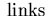 + 2 + 2 |
|
|
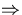 |
2k - 1 |
= |
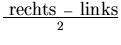 + 1 + 1 |
|
|
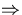 |
2k - 1 - 1 |
= |
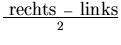 = = 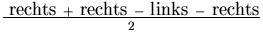 |
|
|
| |
|
= |
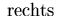 - ( - (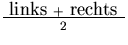 + 1) + 1 + 1) + 1 |
|
|
| |
|
= |
neue Intervalllänge im THEN-Zweig |
|
|
- Korollar:
- 2k - 1 Zahlen verursachen höchstens k Schleifendurchläufe, da nach k Halbierungen die Intervallänge 1 beträgt.
Beispiel für eine Folge von 31 sortierten Zahlen:
| Schleifendurchlauf |
1 |
2 |
3 |
4 |
5 |
| aktuelle Intervalllänge |
25 - 1 |
24 - 1 |
23 - 1 |
22 - 1 |
21 - 1 |
| |
= 31 |
= 15 |
= 7 |
= 3 |
= 1 |
Anders formuliert:
n Zahlen verursachen höchstens 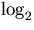 n Schleifendurchläufe.
n Schleifendurchläufe.



Previous: Analyse der Laufzeit der linearen Suche
Up: Lineare und binäre Suche
Next: Klassenmethoden
![]() n Schleifendurchläufe.
n Schleifendurchläufe.