Sortiere die vordere Hälfte der Folge;Die Hilfsroutine zum Mischen lautet: Source: Merge.java JavaDoc: Merge.html
Sortiere die hintere Hälfte der Folge;
Mische die beiden sortierten Folgen zu einer sortierten Folge
Analyse von Mergesort (und ähnlich gelagerten Rekursionen)
f (n) ![]()
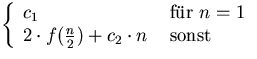
| Beh.: |
f |
| Zeige: |
f (n) |
Verankerung:
|
n = 1 |
f (1) |
|
f (1) |
Induktionsschluss
Sei bis n - 1 bewiesen
| f (n) |
|
| |
|
| Rek. | |
|
|
|
| |
|
| Induktionsannahme | |
|
= 2 · [(c1 + c2) · |
|
| = (c1 + c2)n · logn - (c1 + c2) · n + 2c1 + c2 · n | |
| = [(c1 + c2)n · logn + c1] + [c1 - c1 · n] | |
|
|
Aber: Mergesort benötigt O(n) zusätzlichen Platz!
Iterative Version von Mergesort (für n = 2k)
l = 1; /* Länge der sortierten Teilfolgen */
k = n; /* Anzahl der sortierten Teilfolgen */
while (k > 1) {
/* alle Teilfolgen der Länge l sind sortiert */
/* Sie beginnen bei l · i für
i = 0,1,...,k - 1 */
Mische je zwei benachbarte Teilfolgen der Länge l
zu einer Teilfolge der Länge 2 * l;
l *= 2; k /= 2;
/* Alle Teilfolgen der Länge l sind sortiert */
/* Sie beginnen bei l · i für
i = 0,1,...,k - 1 */
}
Es ergeben sich log n Phasen mit jeweils linearem Aufwand.
![]() O(n · log n)
O(n · log n)
Source:
SortTest.java
JavaDoc:
SortTest.html
Applet:
