Previous: Quicksort
Up: Sortieren
Next: Heapsort
static double select (double[] S, int k) {
/* Liefert aus dem Feld S das k-t kleinste Element. */
/* Das Feld S habe n Elemente. k 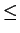 n. */
n. */
double[] A, B, C;
if (|S| < 50) return k-t kleinstes Element per Hand;
else {
n = |S|;
zerlege S in Gruppen zu je 5 Elementen
S1, S2,..., S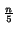 ;
;
Bestimme in jeder Gruppe Si den Median mi;
Bestimme den Median der Mediane:
m = select
(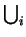 mi,
mi,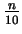 );
);
A = {x 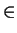 S | x < m};
S | x < m};
B = {x 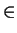 S | x == m};
S | x == m};
C = {x 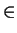 S | x > m};
S | x > m};
if (|A| >= k) return select (A, k);
else if (|A|+|B| >= k) return m;
else /* if (|A|+|B|+|C| >= k) */ return select(C, k-|A|-|B|);
}
}
- Beh.:
-
| A|
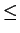
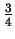 n
n
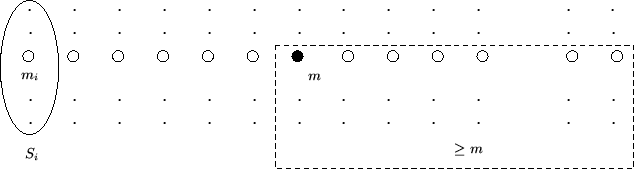
d.h. mind.
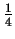 der Elemente von S ist
der Elemente von S ist 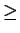 m
m
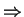 höchstens
höchstens
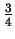 der Elemente von S ist < m
der Elemente von S ist < m
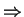 | A|
| A| 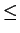
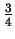 n, analog
| C|
n, analog
| C| 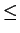
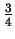 n.
n.
Sei f (n) die Anzahl der Schritte,
die die Methode select benötigt für eine Menge S der
Kardinalität n.
Also:
- Beh.:
-
f
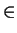 O(n)
O(n)
- Zeige:
-
f (n)
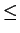 20 . c . n
20 . c . n
Beweis durch Induktion:
f (n) 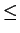 c
c 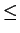 20 . c . n für n < 50
20 . c . n für n < 50
Sei bis n - 1 bewiesen
| f (n) |
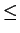 |
c . n |
+ |
f (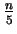 ) ) |
+ |
f (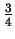 n) n) |
|
| |
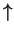 |
|
|
|
|
|
|
| |
Rekursionsgl. |
|
|
|
|
|
|
| |
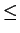 |
c . n |
+ |
20 . c . 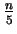 |
+ |
20 . c . 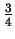 . n . n |
|
| |
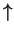 |
|
|
|
|
|
|
| |
Ind.-Annahme |
|
|
|
|
|
|
| |
= |
1 . c . n |
+ |
4 . c . n |
+ |
15 . c . n |
|
| |
= |
20 . c . n |
|
|
|
|
q.e.d. |



Previous: Quicksort
Up: Sortieren
Next: Heapsort