Codierung

Bei der Codierung für 32 Bits (float) benötigt das Vorzeichen 1 Bit, der Exponent 8 Bits, die Mantisse 23 Bits.

X	XXXXXXXX	XXXXXXXXXXXXXXXXXXXXXXX
Vorzeichen $s$	Exponent $e$	Mantisse $f$

$$\mbox{Wert} = \left\{ \begin{array}{lll} (-1)^{s} \times 2^{... ...& \mbox{ falls } e = 0 &\mbox{ (subnormal)} \end{array}\right.$$

Bei einer normalisierten Darstellung liegt der Wert der Mantisse $1.f$ im Intervall $[1, 2[$.

Hierbei haben Dualzahlen nach dem Komma

$$0. d_{-1}d_{-2}d_{-3}\ldots d_{-k} \mbox{ die Bedeutung } \sum_{i = -k}^{-1} d_{i} {\cdot} 2^i$$

Algorithmus dezimal $\rightarrow$ dual:

Sei Dezimalzahl $x$ gegeben. Bestimme größte $2$-er Potenz $2^d$ mit $2^d \leq x$. Setze $f = (x - 2^{d})/2^{d}$. Offenbar gilt

$$x = (1 + f) {\cdot} 2^{d} \mbox{ mit }0 \leq f < 1 .$$

Bestimme die Dualzahl-Bits von $f$ durch

for (i = 0; i < 23; i++) {
   f = f * 2.0;
   if (f >= 1.0) {IO.print('1'); f = f - 1.0;}
      else IO.print('0');
}

Beispiel:

Sei $x = 13.5$ gegeben. Als Codierung ergibt sich

$$\begin{eqnarray*} s&=& {0}\\ f&=& (13.5 - 2^{3})/2^{3} = 0.6875 = \frac{1}{2} + \frac{1}{8} + \frac{1}{16}\\ e&=&3 + 127 = 130 \\ \end{eqnarray*}$$

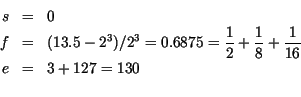
0	10000010	10110000000000000000000
Vorzeichen	Exponent	Mantisse

Bei einer subnormalisierten Darstellung liegt der Wert der Mantisse $0.f$ im Intervall $[0, 1[$.

Exponent $e = 0$ und Mantisse $f = 0$ repräsentieren die vorzeichenbehaftete Null. Exponent $e = 255$ und Mantisse $f = 0$ repräsentieren das vorzeichenbehaftete Unendlich( $+\infty, -\infty$). Exponent $e = 255$ und Mantisse $f \neq 0$ repräsentieren die undefinierte Zahl NaN (not a number).

Beispiel: $2^{-130} = 1/16 {\cdot} 2^{-126}$

Daraus folgt

$$\begin{eqnarray*} s&= & {0}\\ f & = &0.0625\ = \ 1/16\\ e & = & {0} \end{eqnarray*}$$

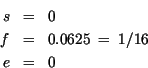
Codierung

0	00000000	00010000000000000000000
Vorzeichen	Exponent	Mantisse

Die größte darstellbare positive Zahl liegt knapp unter

$$2 {\cdot} 2^{254-127} = 2^{128} \approx 10^{38}$$

0	11111110	11111111111111111111111
Vorzeichen	Exponent	Mantisse

Die kleinste darstellbare positive Zahl lautet

$$2^{-23} {\cdot} 2^{-126} = 2^{-149} \approx 10^{-45}$$

0	00000000	00000000000000000000001
Vorzeichen	Exponent	Mantisse

Bei der Codierung für 64 Bits (double) benötigt das Vorzeichen 1 Bit, der Exponent 11 Bits, die Mantisse 52 Bits.

X	XXXXXXXXXXX	XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
Vorzeichen $s$	Exponent $e$	Mantisse $f$

$$\mbox{Wert} = \left\{ \begin{array}{lll} (-1)^{s} \times 2^{... ... \mbox{ falls } e = 0& \mbox{ (subnormal) } \end{array}\right.$$

Damit liegt die größte darstellbare positive Zahl knapp unter

$$2 \cdot 2^{2046 - 1023} \approx 10^{308}$$

Die kleinste darstellbare positive Zahl lautet

$$2^{-52} \cdot 2^{-1022} = 2^{-1074} \approx 10^{-324}$$