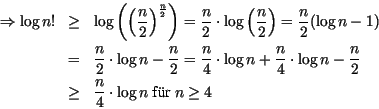Previous: Heapsort
Up: Sortieren
Next: Bucket Sort
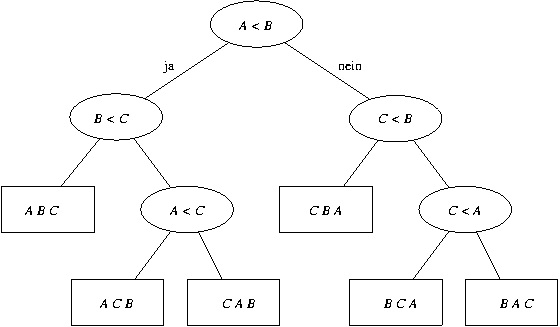
Entscheidungsbaum zur Sortierung von 3 Elementen:
gegeben 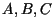
Der Entscheidungsbaum zur Sortierung von 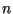 Elementen
hat
Elementen
hat 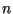 ! Blätter.
! Blätter.
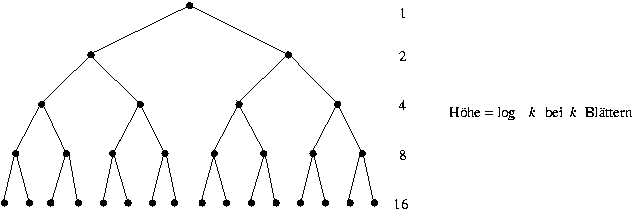
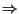
- Ein binärer Baum mit
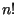 Blättern hat mindestens
die Höhe
Blättern hat mindestens
die Höhe
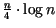 .
.
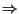
- Jeder Sortieralgorithmus, der auf Vergleichen beruht, hat als Laufzeit
mindestens
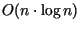 . Dies ist eine untere Schranke.
. Dies ist eine untere Schranke.



Previous: Heapsort
Up: Sortieren
Next: Bucket Sort
![]()

![]() Elementen
hat
Elementen
hat ![]() ! Blätter.
! Blätter.