Geschlossenes Hashing

    private Comparable[] inhalt;           // Array von Comparables 
    private byte[] zustand;                // Array von Zustaenden
                                           // LEER, BELEGT und GELOESCHT

Falls $y=f(x)$ schon belegt ist, so suche für $x$ einen Alternativplatz.

$y+1,y+2,y+3,y+4,\ldots$	lineares Sondieren
$y+1,y+4,y+9,y+16,\ldots$	quadratisches Sondieren
$y+f_{2}(x)$	Double Hashing (Schrittweite wird durch 2. Hashfunktion bestimmt)

Beim linearen und quadratischen Sondieren müssen höchstens $N-1$ Sondierschritte durchgeführt werden. Beim quadratischen Sondieren werden ggf. nicht alle Buckets besucht, aber mindestens $\frac{N}{2}$. Implementation des geschlossenen Hashings

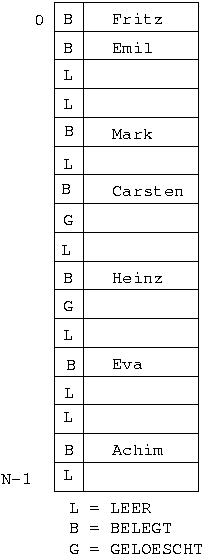
Beispiel:

Die beiden Abbildungen ergeben sich durch sukzessives Einfügen der Worte

Fritz, Mark, Emil, Carsten, Ulf, Heinz, Lutz, Eva, Achim

und anschließendes Löschen von

Ulf, Lutz

für $N = 17$.

Perfekte Hashfunktion

Gesucht wird eine Hashfunktion $f$, die auf den Elementen keine Kollision verursacht, z.B.:

gesucht: $f$	:	{braun,	rot,	blau,	violett,	türkis}	$\rightarrow$	$\mathbb{N}$
Länge$(w)$	=	5	3	4	7	6
Länge$(w)-3$	=	2	0	1	4	3

$\Rightarrow f(w)=$ Länge $(w)-3\in [0..4]$ ist perfekte Hashfunktion.

Source: OfHashing.java     JavaDoc: OfHashing.html    

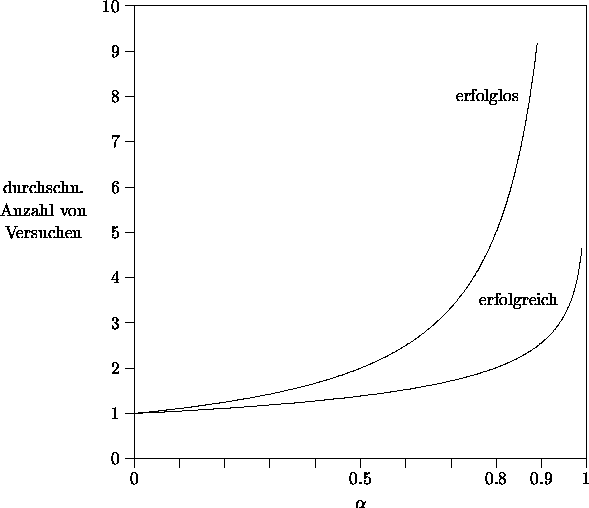
Source: GeHashing.java     JavaDoc: GeHashing.html     Source: HashTest.java     JavaDoc: HashTest.html     Applet: Laufzeit bei geschlossenem Hashing

Sei $n$ die Anzahl der in der Hashtabelle zur Zeit gespeicherten Objekte, sei $N$ die Anzahl der möglichen Speicherpositionen.

Sei $\alpha = \frac{n}{N} \leq 1$ der Auslastungsfaktor.

Dann ergibt sich für die Anzahl der Schritte mit Double-Hashing als Kollisionsstrategie bei

• erfolgloser Suche: $\approx \frac{1}{1- \alpha} = 5.0$, für $\alpha = 0.8$
• erfolgreicher Suche: $\approx - \frac{ln(1 - \alpha )}{\alpha} = 2.01$, für $\alpha = 0.8$

d.h., in 2 Schritten wird von 1.000.000 Elementen aus einer 1.250.000 großen Tabelle das richtige gefunden. (Zum Vergleich: der AVL-Baum benötigt dafür etwa 20 Vergleiche.)