Gleitkommazahlen werden durch Vorzeichen, Mantisse und Exponent beschrieben
und erreichen damit deutlich größere Absolutwerte als Integerzahlen
und können auch gebrochene Zahlen codieren.
Genauer: Für eine gegebene Zahl ![]() werden
Mantisse
werden
Mantisse ![]() und Exponent
und Exponent ![]() gesucht mit der Eigenschaft
gesucht mit der Eigenschaft
Java verwendet zur Kodierung von Vorzeichen, Mantisse und Exponent den IEEE-Standard 754-1985, den wir hier aus didaktischen Gründen etwas vereinfacht darstellen.
Codierung
Bei einer Codierung für 32 Bits (float) werden für das Vorzeichen 1 Bit, für den Exponenten 8 Bits und für die reduzierte Mantisse 23 Bits vorgesehen.
| X | XXXXXXXX | XXXXXXXXXXXXXXXXXXXXXXX |
| Vorzeichen |
Exponent |
reduzierte Mantisse |
Die Codierung des Vorzeichens geschieht über 0 = positiv und 1 = negativ,
die Codierung des ganzzahligen Exponenten erfolgt im 2-er Komplement,
die Codierung der nichtganzzahligen Mantisse erfolgt als Dualzahl mit
Nachkommastellen. Hierbei werden die Dualziffern nach
dem Komma gewichtet mit 2er-Potenzen der Form ![]() mit negativen
mit negativen ![]() .
D.h.
.
D.h.

Zu gegebenem ![]() lässt sich
eine normalisierte Mantisse und der dazu passende Exponent
wie folgt finden:
lässt sich
eine normalisierte Mantisse und der dazu passende Exponent
wie folgt finden:
Bestimme die größte ![]() -er Potenz
-er Potenz ![]() mit
mit ![]() .
Setze
.
Setze ![]() .
Offenbar gilt
.
Offenbar gilt
Zur Bestimmung der ![]() Nachkommastellen der reduzierten Mantisse
Nachkommastellen der reduzierten Mantisse ![]() eignet sich folgender Algorithmus
eignet sich folgender Algorithmus
for (i = 0; i < k; i++) {
f = f * 2.0;
if (f >= 1.0) {IO.print('1'); f = f - 1.0;}
else IO.print('0');
}
Als Codierung ergibt sich
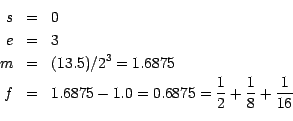
| 0 | 00000011 | 10110000000000000000000 |
| Vorzeichen | Exponent | reduzierte Mantisse |
Für die Spezialfälle wird vereinbart: Das vorzeichenbehaftete
Unendlich (![]() ) wird durch den maximal möglichen Exponent
) wird durch den maximal möglichen Exponent ![]() kodiert. Die vorzeichenbehaftete Null wird durch den minimal möglichen
Exponent
kodiert. Die vorzeichenbehaftete Null wird durch den minimal möglichen
Exponent ![]() kodiert.
kodiert.
Die größte darstellbare positive Zahl im vereinfachten
float-Format liegt knapp unter
| 0 | 01111110 | 11111111111111111111111 |
| Vorzeichen | Exponent | reduzierte Mantisse |
| 0 | 10000001 | 00000000000000000000000 |
| Vorzeichen | Exponent | reduzierte Mantisse |
Bei der Codierung für 64 Bits (double) sind für das Vorzeichen 1 Bit, für den Exponenten 11 Bits und für die reduzierte Mantisse 52 Bits vorgesehen.
| X | XXXXXXXXXXX | XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX |
| Vorzeichen |
Exponent |
reduzierte Mantisse |
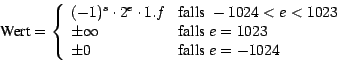
Damit liegt die größte darstellbare positive Zahl im vereinfachten
double-Format knapp unter
Die kleinste darstellbare positive Zahl im vereinfachten double-Format lautet