


Previous: Mergesort
Up: Sortieren
Next: Bestimmung des Medians
Source:
QuickSort.java
JavaDoc:
QuickSort.html
Die Analyse der Laufzeit von Quicksort stützt sich auf folgende
Rekursionsungleichung
für die Anzahl der Schritte 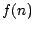 bei
bei 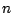 zu sortierenden Daten im
günstigsten Fall (Partitionen sind immer gleich groß):
zu sortierenden Daten im
günstigsten Fall (Partitionen sind immer gleich groß):
Daraus ergibt sich
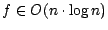 . Diese Komplexität
gilt auch für den durchschnittlichen Fall; es lässt sich
zeigen, dass die Zahl der Schritte
nur um den konstanten Faktor 1.4 wächst.
. Diese Komplexität
gilt auch für den durchschnittlichen Fall; es lässt sich
zeigen, dass die Zahl der Schritte
nur um den konstanten Faktor 1.4 wächst.
Im ungünstigsten Fall (bei entarteten Partitionen) gilt
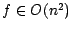 .
.
Source:
QuickSortTest.java
JavaDoc:
QuickSortTest.html
Applet:




Previous: Mergesort
Up: Sortieren
Next: Bestimmung des Medians
![]() . Diese Komplexität
gilt auch für den durchschnittlichen Fall; es lässt sich
zeigen, dass die Zahl der Schritte
nur um den konstanten Faktor 1.4 wächst.
. Diese Komplexität
gilt auch für den durchschnittlichen Fall; es lässt sich
zeigen, dass die Zahl der Schritte
nur um den konstanten Faktor 1.4 wächst.
![]() .
.
