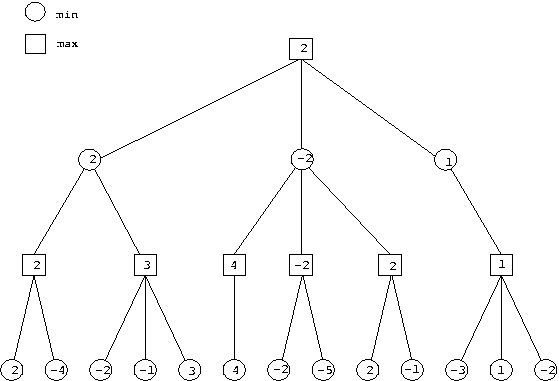
Beispiel für einen Spielbaum

Typischerweise werden die Knoten eines Spielbaums dynamisch während des Spielverlaufs erzeugt. In einem Zwei-Personen-Spiel mit den Spielern Schwarz und Weiß möge ein numerischer Wert die Qualität einer Stellung bezeichnen: positive Werte seien vorteilhaft für Schwarz (der bei den MAX-Knoten am Zuge ist), negative Werte seien vorteilhaft für Weiß (der bei den MIN-Knoten am Zuge ist). Die Entscheidung, ob ein Knoten als Blatt betrachtet wird, hängt von der Spielstellung und auch von der verfügbaren Rechenzeit ab. Wir setzen folgende Klasse voraus:
/************************ Stellung.java ***************************************/
public class Stellung {
... // Datenstrukturen fuer eine Spielstellung
public boolean blatt() { // true, falls Stellung ein Blatt ist
... // false, falls Stellung kein Blatt ist
}
public boolean maxtyp(){ // true, falls MAX-Knoten
... // false, falls MIN-Knoten
}
public int wert() { // liefert statische Stellungsbewertung
...
}
public Liste folgeStellungen() { // erzeugt alle legalen Folgestellungen
...
}
}
Zur Berechnung des sogenannten minmax-Wertes eines Knotens werden rekursiv die minmax-Werte seiner Söhne berechnet, sofern solche vorhanden sind. Andernfalls wird eine statische Stellungsbewertung durchgeführt, welche nicht in die Tiefe geht, sondern die vorhandene Stellung analysiert. Hinweis: Um das minmax-Prinzip zu verdeutlichen, wurde in der folgenden Methode darauf verzichtet, zusätzlich zum Wert der besten Nachfolgestellung auch den dorthinführenden Zug zu vermerken.
/*************************** SpielBaum.java *********************************/
/** Klasse Spielbaum mit der Methode minmax zum Auswerten einer Stellung */
public class SpielBaum {
public static int minmax (Stellung s) { // wertet Stellung aus
if (s.blatt()) // falls Blatt
return s.wert(); // berechne statische Bewertung
else { // andernfalls
Liste l = s.folgeStellungen(); // berechne Folgestellungen
int best= s.maxtyp() ? Integer.MIN_VALUE // best = -unendlich
: Integer.MAX_VALUE; // best = +unendlich
while (!l.endpos()){ // solange es Soehne gibt
Stellung sohn = (Stellung)l.elem(); // naechster sohn
int wert = minmax(sohn); // bestimme Wert der Stellung
if ((s.maxtyp() && wert > best) || // falls Verbesserung
(!s.maxtyp() && wert < best)) // beobachtet wurde
best = wert; // merke Verbesserung
l.advance(); // gehe zum naechsten Bruder
}
return best; // liefere Optimum zurueck
}
}
}