Graphalgorithmen für Adjazenzlisten

Grundlage der folgenden Implementationen sind die Klassen Vertex und Edge. Vertex speichert den Namen des Knoten und seine Nachbarn als Liste von Kanten. Weiterhin gibt es Instanzvariablen zum Speichern von Knoten bezogenen Zwischenergebnissen, die in den verschiedenen Graph-Algorithmen berechnet werden. Die Klasse Edge speichert die Kosten der Kante und einen Verweis auf den Zielknoten.

Graphen werden als eine Assoziation zwischen den Knotennamen und den Knoten-Objekten realisiert, d.h., es kommt aus dem Java Collection Framework eine HashMap<String,Vertex> zum Einsatz, die zu einem gegebenen Knotennamen direkt den zugehörigen Knoten ermitteln kann.

Die Klasse GraphTraverse führt auf einem gerichteten Graphen eine rekursiv organisierte Tiefensuche durch und vergibt Nummern an Knoten in der Reihenfolge, in der sie besucht werden. Bei nicht zusammenhängenden Graphen muß dazu die Suche mehrfach gestartet werden.

Die Klasse TopoSort führt auf einem gerichteten Graphen eine sogenannte topologische Sortierung durch und versucht eine Knoten-Nummerierung f : V $\rightarrow \Bbb{N}$ zu finden, die mit den Kantenrichtungen kompatibel ist, d.h. $(x,y) \in E \Rightarrow f(x) < f(y)$. Begonnen wird bei einem Knoten mit Eingangsgrad 0 (der die erste Nummer erhalten kann). Sei $x$ der Knoten, der zuletzt numeriert wurde. Dann werden nun von $x$ ausgehenden Kanten (virtuell) entfernt und somit die (virtuellen) Eingangsgrade der von ihm erreichbaren Knoten vermindert. Verwendet wird dabei eine Schlange, welche solche Knoten speichert, deren virtueller Eingangsgrad im Laufe der Berechnung inzwischen auf 0 gesunken ist und daher für die nächste zu vergebene Nummer infrage kommen.

Die Klasse Dijkstra löst auf einem gerichteten, mit nichtnegativen Kosten bewerteten Graphen das sogenannte single-source-shortest-path-Problem. D.h., zu einem gegebenen Startknoten werden die kürzesten Wege zu allen anderen Knoten berechnet. Verwendet wird dabei eine Priority-Queue, welche die vorläufige Distanz eines Weges vom Startknoten zu einem Zielknoten in Form einer mit dieser Distanz bewerteten Kante speichert. Zu Beginn haben alle Knoten die vorläufige Distanz $\infty$; der Startknoten erhält die endgültige Distanz 0. Jeweils der billigste Knoten aus der Prioritäts-Schlange kann seine endgültige Distanz erhalten und fügt ggf. die durch ihn verkürzten vorläufigen Distanzen zu seinen Nachbarn in Form von Kanten in die Schlange ein. Weil die Priority-Queue die Kosten der in ihr gespeicherten Wege nicht verringern kann, werden Wege, deren Kosten sich verringert haben, als neue Kanten eingefügt und die Schlange enthält daher für manche Knoten Mehrfacheinträge mit unterschiedlich teuren Kanten. Solche Einträge können nach dem Entfernen aus der Schlange ignoriert werden, wenn der Knoten inzwischen als besucht (seen) markiert wurde.

Die Klasse Hamilton sucht auf einem gerichteten Graphen nach einem Hamilton-Kreis. Das ist ein Rundweg, der jeden Knoten genau einmal besucht und beim Ausgangsknoten wieder endet. Verwendet wird dabei ein Keller von Adjazenzlisten zur Organisation eines Backtracking-Ansatzes. Um die Exploration bei einer oben auf dem Keller liegenden teilweise abgearbeiteten Adjazenzliste an der richtigen Stelle fortführen zu können, bestehen die Kellereinträge aus den Iteratoren der Adzazenzlisten. Diese können jeweils den nächsten, noch nicht ausprobierten Nachbarn liefern.

Die Klasse GraphIO liest einen Graph aus einer Datei ein und zeigt seine Adjazenzlisten an.

Die Klasse Result enthält Routinen zum Anzeigen einer Lösung, welche von dem jeweiligen Algorithmus in den Arbeitsvariablen der Knoten hinterlegt wurde.

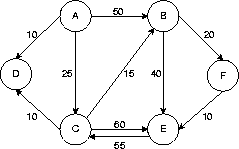
gerichteter, bewerteter Graph: gezeigt sind Knotennamen und Kantenkosten

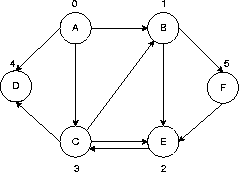
Rekursive Tiefensuche: Numerierung entstanden durch Startknoten A

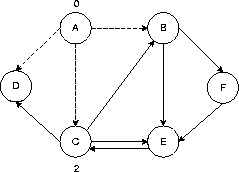
Topologisches Sortieren: Knoten A ist numeriert, Nachfolgekanten entfernt

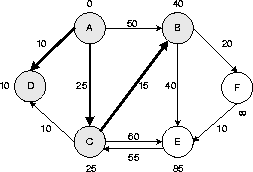
Single-Source-Shortest-Path: Grau gefärbt sind bereits markierte Knoten

Suche nach Hamiltonkreis: markiert ist der aktuelle Weg.
Im Keller liegen Iteratoren für Adjazenzlisten, ihr Fortschritt ist markiert mit #

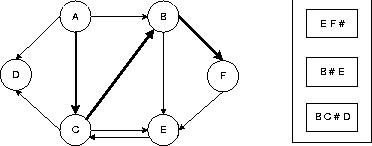
Source: Vertex.java     JavaDoc: Vertex.html     Source: Edge.java     JavaDoc: Edge.html     Source: Graph.java     JavaDoc: Graph.html     Source: GraphTest.java     JavaDoc: GraphTest.html     Applet: Source: GraphTraverse.java     JavaDoc: GraphTraverse.html     Source: TopoSort.java     JavaDoc: TopoSort.html     Source: Dijkstra.java     JavaDoc: Dijkstra.html     Source: Hamilton.java     JavaDoc: Hamilton.html     Source: GraphIO.java     JavaDoc: GraphIO.html     Source: Result.java     JavaDoc: Result.html    

Eingabedatei graph.dat mit Graphbeschreibung

A B 50
A C 25
A D 10
B E 85
B F 20
C B 15
C D 10
C E 60
E C 25
F E 10

von GraphTest.java erzeugte Ausgabe result.dat

Adjazenzlisten des Graphen:

(A,B)50.0  (A,C)25.0  (A,D)10.0  
(F,E)10.0  
(C,B)15.0  (C,D)10.0  (C,E)60.0  
(B,E)85.0  (B,F)20.0  
(E,C)25.0  

Traversierungsreihenfolge:
D erhaelt Nr. 0
A erhaelt Nr. 1
F erhaelt Nr. 5
C erhaelt Nr. 4
B erhaelt Nr. 2
E erhaelt Nr. 3

Graph kann nicht sortiert werden

Der kuerzeste Weg (mit Gesamtkosten 70.0) lautet: 
A -> C -> B -> F -> E

Graph hat keinen Hamiltonkreis