Codierung

Codierung der positiven Zahlen in Dualzahldarstellung:

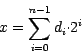
Sei

$$x = \sum_{i=0}^{n-1} d_{i} {\cdot} 2^{i}$$

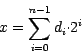
Algorithmus dezimal $\rightarrow$ dual:

while (x != 0){
   if (x%2 == 0) IO.print('0');
            else IO.print('1');
   x = x/2;
}

Obacht: Bits werden rückwärts generiert!

Codierung der ganzen Zahlen im 2-er Komplement:

$d_3$	$d_2$	$d_1$	$d_0$	x
0	1	1	1	7
0	1	1	0	6
0	1	0	1	5
0	1	0	0	4
0	0	1	1	3
0	0	1	0	2
0	0	0	1	1
0	0	0	0	0
1	1	1	1	-1
1	1	1	0	-2
1	1	0	1	-3
1	1	0	0	-4
1	0	1	1	-5
1	0	1	0	-6
1	0	0	1	-7
1	0	0	0	-8

Beispiel zur Berechnung des 2-er Komplements einer negativen Zahl:

Gegeben $-x$	-4
Finde $d_i$ zu $x$	0100
Invertiere Bits	1011
Addiere $1$	1100

Vorteil: Nur ein Addierwerk!

0011	3
+ 1011	-5
= 1110	-2

Subtraktion mittels Negierung auf Addition zurückführen. Obacht: Überlauf beachten!

0111	7
+ 0001	1
= 1000	-8	falsch

Trick: Vorzeichenbits verdoppeln, müssen nach der Verknüpfung identisch sein:

00111	7	00011	3
+ 00001	1	11011	-5
01000		11110	-2
Ergebnis undefiniert		Ergebnis ok!