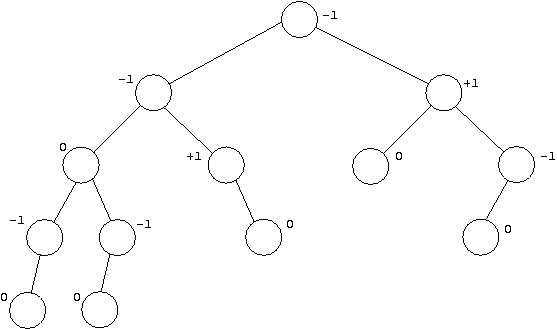
Sei ![]() Höhe des rechten Teilbaums von
Höhe des rechten Teilbaums von ![]() minus Höhe des
linken Teilbaums von
minus Höhe des
linken Teilbaums von ![]() .
.
Aufgrund der Ausgeglichenheit ist die Suche
in einem AVL-Baum auch im ungünstigsten Fall von der Ordnung
![]() .
Um das zu gewährleisten, muss nach jedem Einfügen oder
Löschen die Ausgeglichenheit überprüft und ggf. wiederhergestellt
werden.
Hierzu werden längs des Weges vom eingefügten bzw. gelöschten Element bis zur Wurzel die Balance-Werte
abgefragt und durch so genannte Rotationen repariert.
.
Um das zu gewährleisten, muss nach jedem Einfügen oder
Löschen die Ausgeglichenheit überprüft und ggf. wiederhergestellt
werden.
Hierzu werden längs des Weges vom eingefügten bzw. gelöschten Element bis zur Wurzel die Balance-Werte
abgefragt und durch so genannte Rotationen repariert.
Während das Einfügen eines einzelnen Schlüssels höchstens eine Rotation erfordert, kann das Löschen eine Rotation für jeden Knoten entlang des Weges zur Wurzel verursachen.
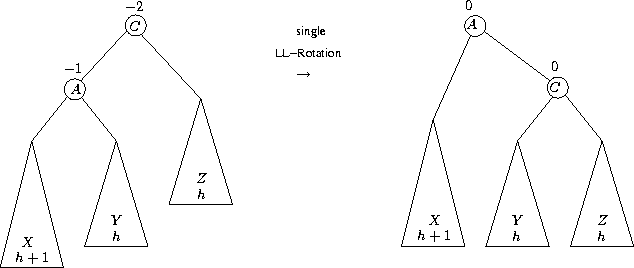
Rotationen für AVL-Baum bei linksseitigem Übergewicht
Single LL-Rotation
Bei Einfügen in Teilbaum ![]() : Höhe des gesamten Baums vorher und nachher gleich.
: Höhe des gesamten Baums vorher und nachher gleich.
Bei Löschen im Teilbaum ![]() : Höhe des gesamten Baums vorher und nachher
gleich oder nachher um eins kleiner.
: Höhe des gesamten Baums vorher und nachher
gleich oder nachher um eins kleiner.
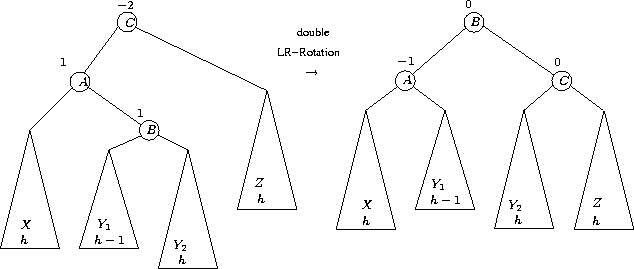
Double LR-Rotation
Bei Einfügen in Teilbaum ![]() oder
oder ![]() : Höhe des gesamten Baums vorher und nachher gleich.
: Höhe des gesamten Baums vorher und nachher gleich.
Bei Löschen im Teilbaum ![]() : Höhe des gesamten Baums nachher um eins kleiner.
: Höhe des gesamten Baums nachher um eins kleiner.
Bei rechtsseitigem Übergewicht werden die symmetrischen Rotationen ``single RR'' und ``double RL'' angewendet.
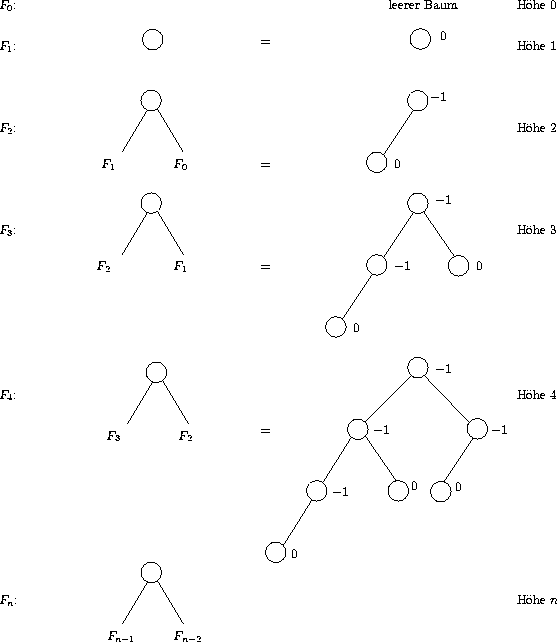
Minimal ausgeglichene AVL-Bäume sind Fibonacci-Bäume
Source:
AVLBaum.java
JavaDoc:
AVLBaum.html
Source:
AVLBaumTest.java
JavaDoc:
AVLBaumTest.html
Applet:
