Geschlossenes Hashing

    private Comparable[] inhalt;           // Array von Comparables 
    private byte[] zustand;                // Array von Zustaenden
                                           // LEER, BELEGT und GELOESCHT

Falls $y=f(x)$ schon belegt ist, so suche für $x$ einen Alternativplatz.

$y+1,y+2,y+3,y+4,\ldots$	lineares Sondieren
$y+1,y+4,y+9,y+16,\ldots$	quadratisches Sondieren
$y+f_2(x), y+2 \cdot f_2(x), ...$	Double Hashing (Schrittweite wird durch 2. Hashfunktion bestimmt)

Alle Berechnungen werden jeweils $mod(N)$ durchgeführt. Insgesamt werden höchstens $N-1$ Sondierschritte verursacht. Beim quadratischen Sondieren werden ggf. nicht alle Buckets besucht, aber mindestens $\frac{N}{2}$. Implementation des geschlossenen Hashings

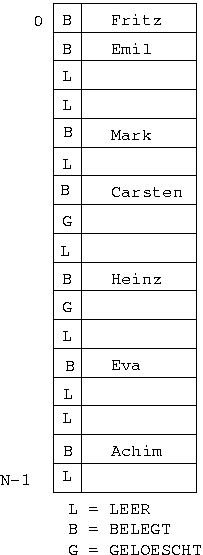
Beispiel:

Die beiden Abbildungen ergeben sich durch sukzessives Einfügen der Worte

Fritz, Mark, Emil, Carsten, Ulf, Heinz, Lutz, Eva, Achim

und anschließendes Löschen von

Ulf, Lutz

für $N = 17$.

Perfekte Hashfunktion

Gesucht wird eine Hashfunktion $f$, die auf den Elementen keine Kollision verursacht, z.B.:

gesucht: $f$	:	{braun,	rot,	blau,	violett,	türkis}	$\rightarrow$	$\mathbb{N}$
Länge$(w)$	=	5	3	4	7	6
Länge$(w)-3$	=	2	0	1	4	3

$\Rightarrow f(w)=$ Länge $(w)-3\in [0..4]$ ist perfekte Hashfunktion.

/*****************************  OfHashing.java  *******************************/
/** Implementation des Interface Menge durch Array von Listen                 */

public class OfHashing implements Menge {

  private Liste[] b ;                       // Array fuer Listen 

  public OfHashing(int N) {                 // Konstruktor fuer Hashtabelle
    b  = new Liste[N];                      // besorge Platz fuer N Listen  
    for (int i=0; i<N; i++)                 // konstruiere pro Index
        b[i]=new VerweisListe();            // eine leere Liste 
  }

  ...                                       // Hilfsmethoden

public Comparable lookup(Comparable x) {  // versucht x nachzuschlagen
    ...
  }
  public boolean insert(Comparable x) {     // versucht x einzufuegen 
    ...
  }
  public boolean delete(Comparable x) {     // versucht x zu loeschen
    ...
  }
}

/*****************************  GeHashing.java  *******************************/
/** Implementation des Interface Menge mit einem Array von Objekten           */

public class GeHashing implements Menge {

  private final static byte LEER      = 0;  // noch nie belegt, jetzt frei
  private final static byte BELEGT    = 1;  // zur Zeit belegt
  private final static byte GELOESCHT = 2;  // war schon mal belegt, jetzt frei

  private Comparable[] inhalt;              // Array fuer Elemente
  private byte[]       zustand;             // Array fuer Zustaende

  public GeHashing(int N) {                 // Konstruktor fuer Hashtabelle
    inhalt  = new Comparable[N];            // besorge Platz fuer N Objekte
    zustand = new byte[N];                  // besorge Platz fuer N Zustaende
    for (int i=0; i<N; i++)                 // setze alle Zustaende
        zustand[i]=LEER;                    // auf LEER 
  }

  ...                                       // Hilfsmethoden
  
  public Comparable lookup(Comparable x) {  // versucht, x nachzuschlagen 
    ...
  }
  public boolean insert(Comparable x) {     // versucht, x einzufuegen 
    ...
  }
  public boolean delete(Comparable x) {     // versucht, x zu loeschen 
    ...
  }
}

Laufzeit bei geschlossenem Hashing

Sei $n$ die Anzahl der in der Hashtabelle zur Zeit gespeicherten Objekte, sei $N$ die Anzahl der möglichen Speicherpositionen.

Sei $\alpha = \frac{n}{N} \leq 1$ der Auslastungsfaktor.

Dann ergibt sich für die Anzahl der Schritte mit Double-Hashing als Kollisionsstrategie bei

• erfolgloser Suche: $\approx \frac{1}{1- \alpha} = 5.0$, für $\alpha = 0.8$
• erfolgreicher Suche: $\approx - \frac{ln(1 - \alpha )}{\alpha} = 2.01$, für $\alpha = 0.8$

d.h., in 2 Schritten wird von 1.000.000 Elementen aus einer 1.250.000 großen Tabelle das richtige gefunden. (Zum Vergleich: der AVL-Baum benötigt dafür etwa 20 Vergleiche.)

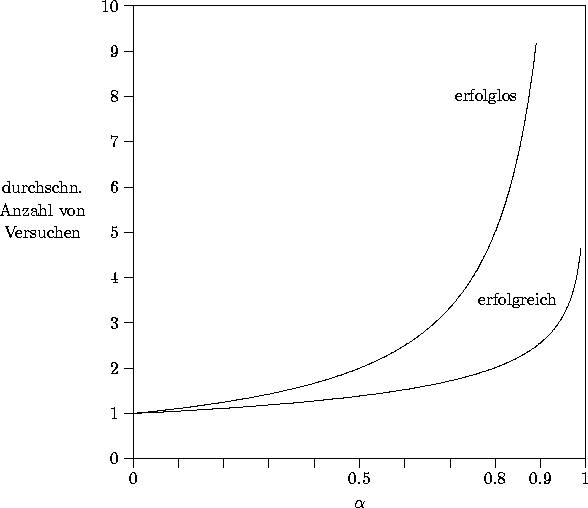
Vergleich mit AVL-Baum

	AVL-Baum	Geschlossenes Hashing
Laufzeit	logarithmisch	konstant
Speicherbedarf	dynamisch wachsend	in Sprüngen wachsend
Sortierung	möglich durch Traversierung	nicht möglich