Graphalgorithmen für Adjazenzmatrizen

Die Klasse Floyd löst das all-pairs-shortest-path-Problem mit dem Algorithmus von Floyd. Für eine $(n\times n)$-Ausgangsmatrix C mit den Kantenkosten werden sukzessive die ($n\times n$)-Matrizen $D^0,~D^1,~D^2, ...,~D^{n-1}$ berechnet. Die Matrix $D^k$ enthält die Kosten der kürzesten Wege zwischen zwei Knoten $i$ und $j$, die als Zwischenknoten nur die Knoten $0, 1, 2, ..., k$ verwenden. Setze $D^{-1}:= C$. Dann lässt sich $D^k_{i,j}$ errechnen durch das Minimum von $D^{k-1}_{i,j}$ und $D^{k-1}_{i,k} + D^{k-1}_{k,j}$.

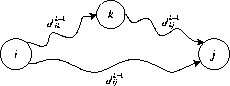
Um auch die zugehörige Kantenfolge rekonstruieren zu können, wird parallel dazu eine Folge von $(n\times n)$-Matrizen $P^0,~P^1,~P^2, ...,~P^{n-1}$ aufgebaut, die an Position $P^k_{i,j}$ den vorletzten Knoten auf dem kürzesten Weg von $i$ nach $j$ notiert, der nur über die Zwischenknoten $0, 1, 2, ..., k$ läuft.

Source: Floyd.java     JavaDoc: Floyd.html     Source: FloydTest.java     JavaDoc: FloydTest.html     Applet: