Maximaler Fluss

Gegeben sei ein gerichteter Graph $G = (V,E)$, gewichtet mit einer Funktion $c:E \to \mathbb{N}$. Die Gewichte $c(i,j)$ werden hier als Kantenkapazitäten interpretiert und beschreiben die maximale Zahl von Transporteinheiten, die pro Zeiteinheit durch diese Kante fließen können. Zwei Knoten aus $V$ sind als Quelle $s$ und die Senke $t$ ausgezeichnet. Modelliert werden mit einem solchen Graph die Transportkapazitäten zwischen diversen Orten und gesucht wird der maximale Fluss, der von der Quelle ausgeht, durch die inneren Knoten fließt und an der Senke ankommt. Dabei muss die Flussmenge, die in einen inneren Knoten hineinfließt, übereinstimmen mit der Flussmenge, die aus ihm herausfließt.

Formal: Sei $V(i)$ die Menge aller Vorgängerknoten von Knoten $i$. Sei $N(i)$ die Menge aller Nachfolgerknoten von Knoten $i$. Ein Fluss ist eine Funktion $f:E \to \mathbb{N}$ mit:

• $0 \le f(i,j) \le c(i,j)$
• für alle $i\in V\backslash\{s,t\}$ gilt: $\sum\limits_{a\in V(i)} f(a,i) =\sum\limits_{b\in N(i)} f(i,b)$,

Gesucht ist nun der maximale Gesamtfluss $F =\sum\limits_{b\in N(s)} f(s,b)= \sum\limits_{a\in V(t)} f(a,t)$.

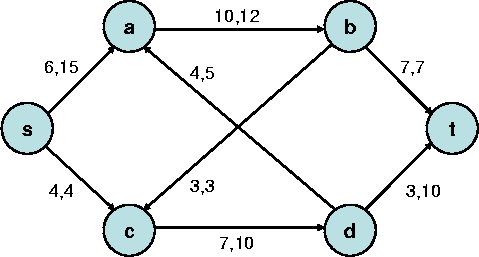
Im folgenden Graph ist jede Kante beschriftet mit ihrem aktuellen Fluss und ihrer maximalen Kapazität. Es fließen insgesamt 10 Einheiten von der Quelle s zur Senke t.

Um den maximalen Fluss zu berechnen, sucht man zunächst sogenannte erweiternde Wege. Ein erweiternder Weg in $G$ ist eine Folge von Knoten, beginnend bei $s$ und endend bei $t$, wobei für zwei aufeinanderfolgende Knoten $i$ und $j$ gilt:

• es existiert eine Vorwärtskante $(i,j)\in E$ mit $f(i,j)<c(i,j)$ oder
• es existiert eine Rückwärtskante $(j,i)\in E$ mit $f(j,i) >0$.

Längs eines erweiternden Weges kann der Fluss vergrößert werden, indem man durch die Vorwärtskanten zusätzliche Einheiten fließen lässt und in den Rückwärtskanten den Fluss verringert.

Der Algorithmus von Ford-Fulkerson versucht solange den aktuellen Fluss längs eines erweiternden Weges zu erhöhen, wie dies möglich ist:

     Sei f = 0 der initiale Fluss;
     repeat {
          Suche bzgl. f einen erweiternden Weg von s nach t;
          falls gefunden: erhöhe f längs dieses Weges;
     } while möglich

Die Korrektheit dieses Algorithmus folgt unmittelbar aus dem folgenden Satz:

Ein Fluss $f$ ist maximal $\iff$ Es gibt keinen erweiternden Weg.

$\Leftarrow$

Sei ein Cut des Graphen $G = (V,E)$ definiert als eine Partition der Knotenmenge $V$ in $S$ und $S'$, so dass gilt: $s\in S$ und $t\in V\backslash S=\overline{S}$. Sei dann $(S,\overline{S}):=\{(x,y)\in E \vert x \in S, y \in\overline{S}\}$. Die Kapazität eines Cuts ist dann festgelegt durch $c(S):=\sum\limits_{e\in(S,\overline{S})} c(e)$.

Daraus folgt unmittelbar der folgende Satz:

Sei $f$ ein Fluss der Größe $F$, sei $S$ ein Cut von $G$

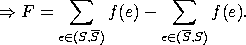
Der Fluss ist also an jedem beliebigen Cut messbar. Aus diesem Satz folgt aber direkt:

Sei $f$ ein Fluss der Größe $F$, sei $S$ ein Cut von $G$

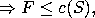
d.h. der Fluss ist höchstens so hoch wie die Kapazität eines Cuts.

$\Rightarrow$

Ist ein Fluss $f$ so groß wie die Kapazität eines Cuts $S$, so ist $f$ ein maximaler Fluss und $S$ ist ein minimaler Cut bezogen auf seine Kapazität c(S).

Wir betrachten nun folgende Situation:

Es gibt in $G$ keine erweiternden Wege mehr. Dann enden also alle von $s$ ausgehenden erweiternden Wege - genauer gesagt deren Anfangsstücke - entweder bei einer saturierten Vorwärtskante oder bei einer Rückwärtskante mit Fluss 0. Durch diese Kanten wird also ein Cut $S$ impliziert, dessen Kapazität gleich dem momentanen Fluss ist. Daher muss der momentane Fluss aufgrund des letzten Satzes maximal sein.

Die Suche nach einem erweiternden Weg wird durch eine Breitensuche organisiert, die beim Knoten $s$ beginnt:

     Markiere s;
     Sei M := {s} die Menge der noch zu bearbeitenden Knoten;
     while M nicht leer und t ist noch nicht markiert {
          Besorge und entferne aus M einen markierten Knoten x
          IF $\exists$ unmarkiertes y mit (x,y) $\in$ E und f(x,y)<c(x,y) THEN
               markiere y und vermerke bei y seinen Vorgänger x;
               notiere $\delta$(x,y) := c(x,y) - f(x,y);
               nimm y in M auf;
          IF $\exists$ unmarkiertes y mit (y,x) $\in$ E und f(y,x) > 0 THEN
               markiere y und vermerke bei y seinen Vorgänger x;
               notiere $\delta$(x,y) := f(y,x);
               nimm y in M auf;
     }
     fallst t markiert THEN
          berechne ausgehend von t längs der Vorgänger das maximal mögliche $\delta$;
          erhöhe ausgehend von t längs der Vorgänger den Fluss f um $\delta$;

In folgendem Graph ist ein erweiternder Weg fett markiert. Er führt von $s$ über $a$ und $d$ nach $t$ und erlaubt eine Flusserhöhung um $\delta=4$.

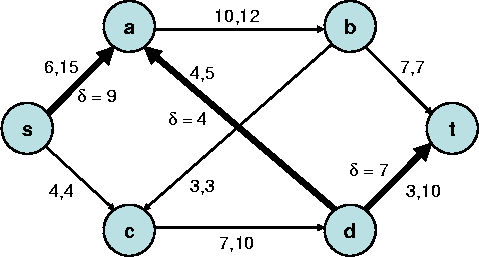
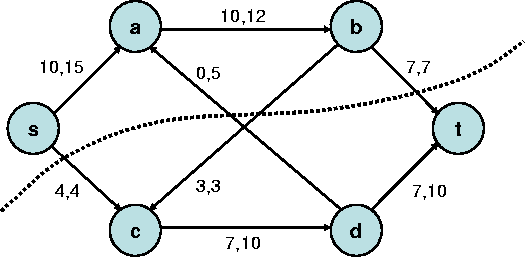
Nach Anwendung des erweiternden Weges entsteht der folgende Graph, mit einem Fluss (und einem Cut) von 14 Einheiten. Da kein weiterer erweiternder Weg existiert, ist der Fluss maximal.

Zur effizienten Implementation der Breitensuche ist es erforderlich, bei jedem Knoten nicht nur die Liste seiner Nachfolger, sondern auch die Liste seiner Vorgänger zu speichern.