| endliche Zustandsmenge | ||
| endliches Eingabealphabet | ||
|
|
Überführungsfunktion | |
| Anfangs- oder Startzustand | ||
| Endzustände |
| endliche Zustandsmenge | ||
| endliches Eingabealphabet | ||
|
|
Überführungsfunktion | |
| Anfangs- oder Startzustand | ||
| Endzustände |
Die Wirkungsweise der Überführungsfunktion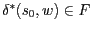
.
Beispiel:
![]() soll durch
soll durch ![]() teilbare Dualzahlen erkennen. Hierzu spendieren
wir drei Zustände mit der Bedeutung Rest 0, Rest 1 und Rest 2.
Folgende Fälle können
auftreten, wenn ein String
teilbare Dualzahlen erkennen. Hierzu spendieren
wir drei Zustände mit der Bedeutung Rest 0, Rest 1 und Rest 2.
Folgende Fälle können
auftreten, wenn ein String ![]() , dessen Rest als 0, 1 oder 2 bekannt ist,
verlängert wird mit dem Zeichen 0 bzw. mit
dem Zeichen 1:
, dessen Rest als 0, 1 oder 2 bekannt ist,
verlängert wird mit dem Zeichen 0 bzw. mit
dem Zeichen 1:
| w | w0 | w1 |
| 3x + 0 | 6x + 0 | 6x + 1 |
| Rest 0 | Rest 0 | Rest 1 |
| 3x + 1 | 6x + 2 | 6x + 3 |
| Rest 1 | Rest 2 | Rest 0 |
| 3x + 2 | 6x + 4 | 6x + 5 |
| Rest 2 | Rest 1 | Rest 2 |
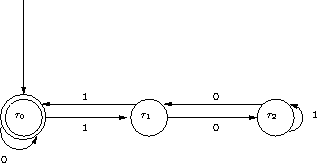
Also ergibt sich folgender Automat:
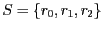
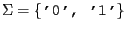
Startzustand ist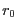
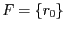
Dazu gehört ein Zustandsüberführungsgraph mit
den Knoten ![]() ,
, ![]() und
und ![]() , welche die Zustände beschreiben,
wenn für den bislang eingelesenen String die Division durch 3
den Rest 0, 1 bzw. 2 ergibt.
An der Kante steht das jeweils nächste Bit der Dualzahl, die von links nach rechts abgearbeitet wird.
, welche die Zustände beschreiben,
wenn für den bislang eingelesenen String die Division durch 3
den Rest 0, 1 bzw. 2 ergibt.
An der Kante steht das jeweils nächste Bit der Dualzahl, die von links nach rechts abgearbeitet wird.