Implementation von Graphen

Es sei jedem Knoten eindeutig ein Index zugeordnet. Für den gerichteten Graphen auf Seite ergibt sich:

Index	Knoten
0	$a$
1	$b$
2	$c$
3	$d$

Implementation durch Adjazenzmatrizen

Unbewertete Kanten:

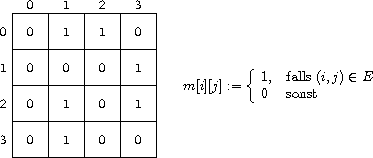
Bewertete Kanten:

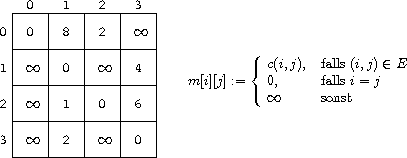
Platzbedarf $=O(\vert V\vert^{2})$.
Direkter Zugriff auf Kante $(i,j)$ in konstanter Zeit möglich.
Kein effizientes Verarbeiten der Nachbarn eines Knotens.
Sinnvoll bei dicht besetzten Graphen, d.h. Graphen mit quadrisch vielen Kanten.
Sinnvoll bei Algorithmen, die wahlfreien Zugriff auf eine Kante benötigen. Implementation durch Adjazenzlisten

Wenn die Knoten des Graphen über ihren Index identifiziert werden, bietet sich zusätzlich zum Namens-Array ein Array von Integer-Listen an. Die an Position $i$ beginnende Liste enthält die Nachbarn von $i$, genauer gesagt, sie enthält die Indizes der Nachbarn von $i$.

Für bewertete Graphen muss ein Listeneintrag innerhalb der $i$-ten Liste neben der Knoten-Nummer j auch die Kosten der Kante $(i,j)$ enthalten. Für den gerichteten Graphen auf Seite ergibt sich:

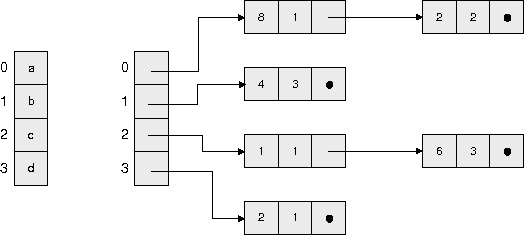
Eine objektorientierte Codierung würde die Knoten als Objekte modellieren, welche ihren Namen als String speichern und ihre Nachbarn als Kantenliste. Die Einträge der Kantenliste bestehen jeweils aus den Kosten der Kante und einem Verweis auf den Knoten. Über ein assoziatives Array (implementiert als Hash-Map) gelangt man vom Namen eines Knotens zu seinem Objekt. Für den gerichteten Graphen auf Seite ergibt sich:

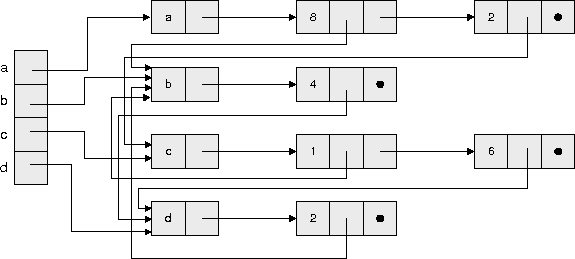
Platzbedarf =$O(\vert E\vert)$
Kein effizienter Zugriff auf Kante $(x,y)$ möglich.
Sinnvoll bei dünn besetzten Graphen, d.h. Graphen mit nur linear vielen Kanten.
Sinnvoll bei Algorithmen, die, gegeben ein Knoten $x$, dessen Nachbarn verarbeiten müssen.