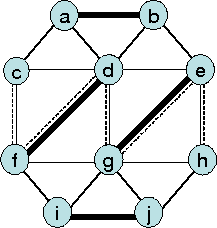
Ein Matching ![]() in einem ungerichteten Graph
in einem ungerichteten Graph ![]() besteht aus einer Menge von unabhängigen Kanten,
d.h. Kanten, die keine gemeinsamen Endknoten haben.
Ein Matching modelliert mögliche
Zuordnungen in einem System von binären Beziehungen, z.B. Spielpartner
in einem Tennisturnier.
besteht aus einer Menge von unabhängigen Kanten,
d.h. Kanten, die keine gemeinsamen Endknoten haben.
Ein Matching modelliert mögliche
Zuordnungen in einem System von binären Beziehungen, z.B. Spielpartner
in einem Tennisturnier.
Bzgl. eines Matchings ![]() wird ein Knoten frei genannt, wenn er nicht
Endpunkt einer Matchingkante ist; der
Knoten heißt belegt, wenn er Endpunkt von (genau) einer Matching-Kante
ist. In einem gewichteten Graphen werden die
Kosten eines Matchings durch die Summe der Gewichte der benutzten Kanten definiert.
wird ein Knoten frei genannt, wenn er nicht
Endpunkt einer Matchingkante ist; der
Knoten heißt belegt, wenn er Endpunkt von (genau) einer Matching-Kante
ist. In einem gewichteten Graphen werden die
Kosten eines Matchings durch die Summe der Gewichte der benutzten Kanten definiert.
![]() ist ein Maximal-Matching, wenn zu
ist ein Maximal-Matching, wenn zu ![]() keine weitere Kante hinzugefügt werden kann.
keine weitere Kante hinzugefügt werden kann.
![]() ist ein Maximum-Matching, wenn es keine anderen Matchings mit mehr Kanten gibt.
ist ein Maximum-Matching, wenn es keine anderen Matchings mit mehr Kanten gibt.
![]() ist ein perfektes Matching, wenn alle Knoten belegt sind.
ist ein perfektes Matching, wenn alle Knoten belegt sind.
![]() ist ein Minimum-Cost-Matching, wenn es von allen perfekten Matchings die geringsten Kosten verursacht.
ist ein Minimum-Cost-Matching, wenn es von allen perfekten Matchings die geringsten Kosten verursacht.
Maximale Matchings können mit einem Greedyverfahren bestimmt werden, indem solange Kanten zwischen freien Knoten gewählt werden, bis dies nicht mehr möglich ist.
Maximum-Matchings können bestimmt werden, indem ausgehend von einem initialen Matching sogenannte
erweiternde Wege gefunden werden, längs derer das Matching vergrößert wird. Genauer: Ein alternierender
Weg bzgl. eines Matchings ![]() ist eine Sequenz von Kanten mit jeweils
gemeinsamen Endpunkten, die abwechselnd zum Matching und nicht
zum Matching gehören. Ein erweiternder Weg bzgl. eines Matchings
ist eine Sequenz von Kanten mit jeweils
gemeinsamen Endpunkten, die abwechselnd zum Matching und nicht
zum Matching gehören. Ein erweiternder Weg bzgl. eines Matchings ![]() ist ein alternierender Weg bzgl.
ist ein alternierender Weg bzgl. ![]() , der bei einem freien Knoten
beginnt und bei einem freien Knoten endet. Durch Umtauschen der Matchingkanten
in Nicht-Matchingkanten und umgekehrt kann längs des erweiternden Weges
das Matching um eine Kante erhöht werden.
, der bei einem freien Knoten
beginnt und bei einem freien Knoten endet. Durch Umtauschen der Matchingkanten
in Nicht-Matchingkanten und umgekehrt kann längs des erweiternden Weges
das Matching um eine Kante erhöht werden.
Es gilt der Satz: