Minimaler Spannbaum

Gegeben ein ungerichteter, gewichter Graph $G = (V,E)$, dessen Kanten mit der Funktion $c: E \rightarrow \mathbb{N}$ gewichtet sind. Gesucht wird eine Teilmenge von Kanten mit möglichst geringen Gesamtkosten, die alle Knoten verbindet. Hat der Graph $n$ Knoten, so besteht der Spannbaum aus $n - 1$ Kanten.

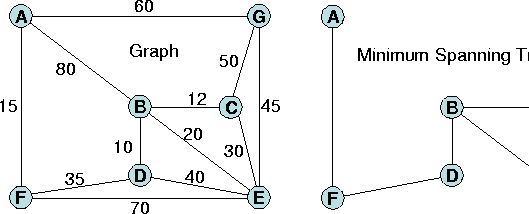
Probleme dieser Art entstehen immer dann, wenn ein kostengünstiges Netzwerk gesucht wird, welches z.B. eine Menge von Inseln durch Brücken oder ein Menge von Ortschaften durch Stromleitungen verbindet.

Ein Lösungsverfahren wurde von Kruskal vorgestellt:

     Initialisiere einen Wald von Bäumen durch n isolierte Knoten;
     Initialisiere einen Heap mit allen gewichteten Kanten;
     while noch nicht genügend Kanten gefunden {
          entferne die billigste Kante (x,y) aus dem Heap;
          falls x und y im verschiedenen Baümen sind;
          vereinige die beiden Bäume;
     }

Die Korrektheit des Kruskal-Algorithmus folgt aus dem folgenden

Satz: Gegeben sei eine Partition $V_1, V_2$ der Knotenmenge $V$. Sei $s$ die billigste Kante zwischen $V_1$ und $V_2$. Dann gibt es einen MSB (Minimaler Spannbaum) der $s$ enthält. ($s$ ist sogar in allen MSBs enthalten).

Beweis:

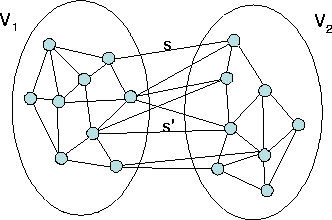
Annahme: $s$ sei nicht im MSB enthalten. Dann füge $s$ in den MSB ein. Es entsteht ein Zyklus, der über $s'$ läuft. Entferne nun $s'$ aus dem MSB. Es entsteht ein neuer, billigerer MSB. Dies ist ein Widerspruch zur Minimalität des Ausgangs-MSB.

Zur Verwaltung der Zusammenhangskomponenten notieren wir bei jedem Knoten $x$ in einer Arbeitsvariable chef denjenigen Knoten, der zur Zeit als Vorgesetzter für ihn fungiert. Ein Knoten, der sein eigener Vorgesetzter ist, übernimmt die Rolle des Repräsentanten für alle Knoten, die in seiner Zusammenhangskomponente liegen und die über die Variable chef direkt oder indirekt auf ihn verweisen. Bei der Vereinigung von zwei Zusammenhangskomponenten mit den Repräsentanten $x$ und $y$ muss nur einer der beiden (z.B. $x$) den anderen (d.h. $y$) als neuen Chef eintragen.

Damit die Suche nach dem aktuellen Chef nicht zu immer länger werdenden Verweisketten führt, benutzt man die Technik des Path halving: Längs des Weges von einem Knoten $x$ zu seinem Repräsentanten $z$ wird bei jedem Knoten der aktuelle Vater durch den Großvater ersetzt. Dieser Mehraufwand zahlt sich insofern aus, als bei der nächsten Repräsentantensuche der Weg nur noch halb so lang ist.

Hat der Graph $n$ Knoten und $m$ Kanten, dann beträgt der Aufwand für den Kruskal-Algorithmus $O(m \cdot \log(m) \cdot$lg*($m$)), da maximal jede Kante einmal mit Aufwand $\log m$ aus dem Heap genommen wird. Der zusätzliche Faktor lg*($m$) bezeichnet eine fast konstante, sehr langsam wachsende Funktion (nämlich die Inverse der Ackermannfunktion, für alle praktischen Werte von $m$ kleiner als 5). Sie wird verursacht durch das Testen mit Path Halving, ob zwei Knoten in derselben Zusammenhangskomponente liegen.

Source: Kruskal.java     JavaDoc: Kruskal.html     Source: KruskalTest.java     JavaDoc: KruskalTest.html     Applet:

von KruskalTest.java erzeugte Ausgabe undiresult.dat

Adjazenzlisten des Graphen:

(D,B)10.0  (D,E)40.0  (D,F)30.0  
(E,B)20.0  (E,C)20.0  (E,D)40.0  (E,F)70.0  (E,G)40.0  
(F,A)20.0  (F,D)30.0  (F,E)70.0  
(G,A)60.0  (G,C)50.0  (G,E)40.0  
(A,B)80.0  (A,F)20.0  (A,G)60.0  
(B,A)80.0  (B,C)10.0  (B,D)10.0  (B,E)20.0  
(C,B)10.0  (C,E)20.0  (C,G)50.0  

Der minimale Spannbaum besteht aus folgenden Kanten:
 
(B,C) 10.0
(B,E) 20.0
(B,D) 10.0
(D,F) 30.0
(A,F) 20.0
(E,G) 40.0