Vorbemerkung: Ein ungerichteter Graph heißt Eulergraph, falls alle Knoten geraden Knotengrad haben. Ein Eulergraph erlaubt immer eine sogenannte Eulertour, d.h. einen geschlossenen Kantenzug, in dem jede Kante genau einmal vorkommt. Die Konstruktion einer Eulertour geschieht durch willkürliches Ablaufen noch nicht benutzter Kanten und nutzt aus, dass ein Knoten, der über eine noch nicht benutzte Kante angelaufen wird, immer (wegen seines graden Knotengrads) eine noch nicht benutzte Kante aufweist, über die der Weg fortgesetzt werden kann. Letztendlich muss diese Kantenfolge wieder beim Ausgangsknoten ankommen. Ggf. müssen mehrere Kantenzüge, die auf diese Weise konstruiert wurden, zu einem Gesamtweg verschmolzen werden.
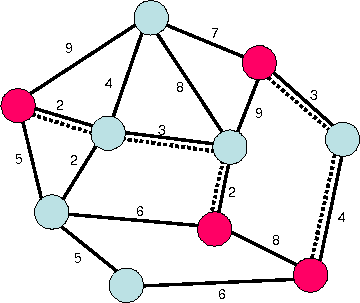
In folgendem Graph haben alle Knoten geraden Grad. Eine erste
Kantenfolge (gestrichelt gezeichnet)
beginnt bei ![]() , läuft dann über
, läuft dann über
![]() und
kehrt zu
und
kehrt zu ![]() zurück. Eine weitere Kantenfolge (gepunktet gezeichnet)
beginnt bei
zurück. Eine weitere Kantenfolge (gepunktet gezeichnet)
beginnt bei ![]() , läuft über
, läuft über
![]() und kehrt zu
und kehrt zu ![]() zurück.
Beide Folgen können z.B. am Knoten
zurück.
Beide Folgen können z.B. am Knoten ![]() verschmolzen werden, indem
die gestrichelte Folge bei Ankunft in H zunächst die gepunktete
Folge abläuft und dann die gestrichelte Folge weiter führt. Es
ergibt sich als Eulertour
verschmolzen werden, indem
die gestrichelte Folge bei Ankunft in H zunächst die gepunktete
Folge abläuft und dann die gestrichelte Folge weiter führt. Es
ergibt sich als Eulertour
![]() .
.
Gegeben sei nun ein ungerichteter Graph ![]() , gewichtet mit einer
Kostenfunktion
, gewichtet mit einer
Kostenfunktion
![]() .
.
Das Problem des Chinese Postman besteht darin, eine billigste Kantenrundreise zu bestimmen, d.h. eine geschlossene, möglichst billige Kantenfolge über alle Knoten, in der jede Kante mindestens einmal auftritt. Dies soll die Aufgabe eines Briefträgers modellieren, der kostengünstig alle Straßen einer Stadt abgehen und wieder zum Ausgangspunkt zurückkehren soll.
Die Lösung dieses Problems hängt mit der Euler-Eigenschaft zusammen:
Offensichtlich wird in einer optimalen Lösung jede Kante maximal zweimal durchlaufen. Denn würde sie öfter durchlaufen, so ließen sich zwei Durchläufe streichen, der Graph bliebe weiterhin eulersch und die Tour wäre verbilligt.
Sei ![]() :=
:=
![]() die Menge der Knoten aus
die Menge der Knoten aus ![]() mit
ungeradem Knotengrad.
Offenbar gilt:
mit
ungeradem Knotengrad.
Offenbar gilt: ![]() ist gerade, denn in einem Graph ist die Anzahl der
Knoten mit ungeradem Kantengrad gerade.
ist gerade, denn in einem Graph ist die Anzahl der
Knoten mit ungeradem Kantengrad gerade.
Auf der Menge ![]() errechne mit dem Algorithmus von Floyd die Distanzmatrix
errechne mit dem Algorithmus von Floyd die Distanzmatrix
![]() , d.h. die Kosten der kürzesten Wege zwischen allen Paaren
aus
, d.h. die Kosten der kürzesten Wege zwischen allen Paaren
aus ![]() unter Verwendung aller Knoten und Kanten aus
unter Verwendung aller Knoten und Kanten aus ![]() .
.
Betrachte nun die Clique dieser ![]() Knoten mit ihren errechneten
Kantengewichten
Knoten mit ihren errechneten
Kantengewichten ![]() .
.
In dieser Clique suchen wir ein Minimum Cost Matching ![]() . Dieses Matching
liefert uns die Knotenpaare, die mit einem kürzesten Weg gemäß Floyd
verbunden werden müssen.
Dadurch erhalten alle Knoten einen geraden Grad.
Wir erhalten also einen Eulergraph, der einen geschlossenen Weg über
alle Kanten erlaubt und damit die gesuchte Postman-Tour darstellt.
. Dieses Matching
liefert uns die Knotenpaare, die mit einem kürzesten Weg gemäß Floyd
verbunden werden müssen.
Dadurch erhalten alle Knoten einen geraden Grad.
Wir erhalten also einen Eulergraph, der einen geschlossenen Weg über
alle Kanten erlaubt und damit die gesuchte Postman-Tour darstellt.
Es lässt
sich nachweisen, dass die zugehörigen Wege alle kantendisjunkt sind. Denn
würde eine Kante ![]() gemeinsam auf dem kürzesten Weg von
gemeinsam auf dem kürzesten Weg von ![]() nach
nach ![]() und von
und von ![]() nach
nach ![]() genutzt, so könnten durch Entfernen der Kante
genutzt, so könnten durch Entfernen der Kante ![]() zwei billigere Wege von
zwei billigere Wege von ![]() über
über ![]() nach
nach ![]() und von
und von ![]() über
über ![]() nach
nach ![]() entstehen.
entstehen.
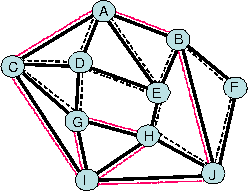
Im folgenden Graphen gibt es vier Knoten mit ungeradem Grad (fett markiert). Sie werden preisgünstig durch kürzeste Wege (gestrichelt markiert) miteinander verbunden. Längs dieser Wege werden nun alle Kanten verdoppelt, so dass dadurch alle Knoten geraden Grad haben. Auf diesem Eulergraph bildet dann eine Eulertour die Lösung des Chinese Postman.