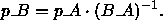Die Transformation von einem Koordinatensystem in ein anderes läßt sich
folgendermaßen formalisieren:
Gegeben sei ein Koordinatensystem A , in dem ein anderes
Koordinatensystem B durch die homogenen Koordinaten des Ursprungs
( Bw ) und die drei Richtungsvektoren der Achsen ( Bx , By , Bz )
definiert ist.
Zeilenweise angeordnet ergeben diese Vektoren die Matrix
B _ A , die den Übergang vom Koordinatensystem B zum
Koordinatensystem A beschreibt:
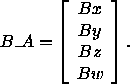

Beispiel (für den 2-dimensionalen Fall):
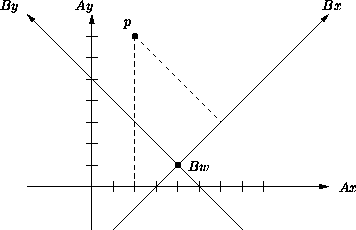
| x -Achse: | Bx | lautet |
[ |
| y -Achse: | By | lautet |
[- |
| Ursprung: | Bw | lautet | [4,1,1] |
| Punkt: | p _ B | lautet |
[2 · |
Also läßt sich der Punkt p wie folgt transformieren:
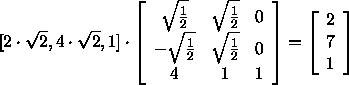
Um einen Punkt p _ A
des Koordinatensystems A im Koordinatensystem B
zu spezifizieren, verwendet man die inverse
Matrix zu B _ A :