3.2 Linie

Problem: Gegeben sind Anfangs- und Endkoordinaten einer Linie. Berechne die ``anzuschaltenden'' Pixel.

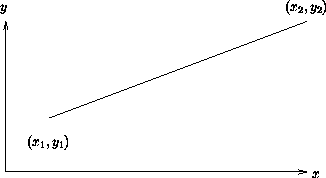
1. Möglichkeit: Bestimme Geradengleichung y = s · x + c
Es gilt:

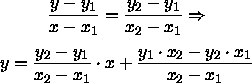
Daraus ergibt sich folgender Algorithmus unter Verwendung der Klasse java.awt.Point mit den beiden Integer-Koordinaten x und y:

    void plot_line(Point P, Point q)
    {
            double s, c;
            Point p = new Point(P);
    
            s = (double) (q.y-p.y) / (double) (q.x-p.x);
            c = (double) (p.y*q.x - q.y*p.x) / (double) (q.x - p.x );
    
            while (p.x <= q.x) {
                    p.y = (int)(s*p.x + c + 0.5);
                    set_pixel(p);
                    p.x++;
            }
    }

Verfahren hat 2 Nachteile:

1.

Pixel für steile Geraden sind nicht benachbart.

2.

viel Gleitkomma-Arithmetik

Lösung: Bresenham-Algorithmus

Idee: Berechne den nächsten y -Wert aus dem vorherigen. Merke den momentanen Fehler.

Zunächst: Gerade verläuft im 1. Oktanten (d.h. Steigung < 1)

    void bresenham_linie_1(Point P, Point q)
    {
            int dx, dy;
            double s, e;
            Point p = new Point(P);
    
            dx    = q.x - p.x;
            dy    = q.y - p.y;
            e     = 0.0;
            s     = (double) dy / (double) dx;
    
            while (p.x <= q.x) {
                    set_pixel(p);
                    p.x++;
                    e += s;
                    if (e > 0.5) { p.y++; e-- ; }
            }
    }

Eliminiere Gleitkommazahlen durch Multiplikation von s mit 2*dx:

    void bresenham_linie_2(Point P, Point q)
    {
            int dx, dy, error, delta;
            Point p = new Point(P);
    
            dx    = q.x - p.x;
            dy    = q.y - p.y;
            error = 0;
            delta = 2*dy;   
    
            while (p.x <= q.x) {
                    set_pixel(p);
                    p.x++;
                    error += delta;
                    if (error > dx) { p.y++; error -= 2*dx; }
    
            }
    }

Vergleiche error mit 0 und verwende Abkürzung schwelle für -2*dx

    void bresenham_linie_3(Point P, Point q)
    {
            int dx, dy, error, delta, schwelle;
            Point p = new Point(P);
    
            dx       = q.x - p.x;
            dy       = q.y - p.y;
            error    = -dx;
            delta    = 2*dy;
            schwelle = -2*dx;
    
            while (p.x <= q.x) {
                    set_pixel(p);
                    p.x++;
                    error += delta;
                    if (error > 0) { p.y++; error += schwelle; }
            }
    }

Geraden in den anderen 7 Oktanten müssen durch Spiegelung und/oder Vertauschen von x und y auf den 1. Oktanten zurückgeführt werden.

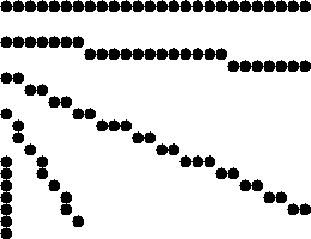
Vom Bresenham-Algorithmus erzeugte Linien

/****************************************************************************************/
/*                                                                                      */
/*                      Bresenham-Algorithmus zum Zeichnen einer Linie                  */
/*                                                                                      */
/****************************************************************************************/

private void bresenham_linie(                  // zeichnet mit Bresenham-Algorithmus
        Point P, Point q)                      // eine Linie von Punkt P nach Punkt q
{
        Point p = new Point(P);

        int error, delta, schwelle, dx, dy, inc_x, inc_y;
        dx = q.x - p.x;
        dy = q.y - p.y;

        if (dx>0) inc_x= 1; else inc_x=-1;
        if (dy>0) inc_y= 1; else inc_y=-1;

        if (Math.abs(dy) < Math.abs(dx)) {     // flach nach oben oder flach nach unten

                error = -Math.abs(dx);
                delta = 2*Math.abs(dy);
                schwelle = 2*error;
                while (p.x != q.x) {
                        set_pixel(p);
                        p.x+=inc_x;
                        error = error + delta;
                        if (error >0) { p.y+=inc_y; error = error + schwelle;}
                }
        } else                                 // steil nach oben oder steil nach unten
        {
                error = -Math.abs(dy);
                delta = 2*Math.abs(dx);
                schwelle = 2*error;
                while (p.y != q.y) {
                        set_pixel(p);
                        p.y+=inc_y;
                        error = error + delta;
                        if (error >0) { p.x+=inc_x; error = error + schwelle;}
                }

        }         
        set_pixel(q);
}