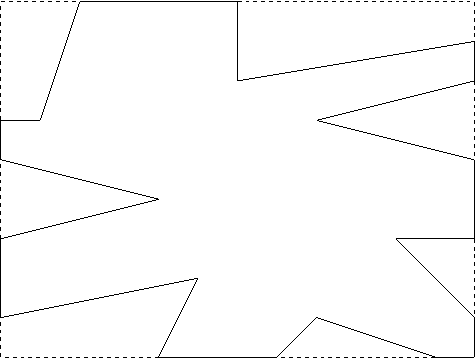

Vielmehr müssen zusätzlich die Ein- und Austrittspunkte verbunden werden, um nach dem Clipping wieder ein Polygon zu erhalten:
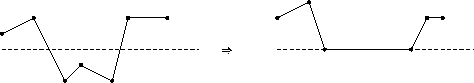
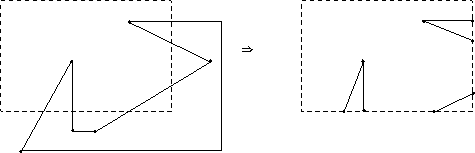
Obacht: Bzgl. der Ecken des Clip-Windows ist eine Spezialbehandlung erforderlich:
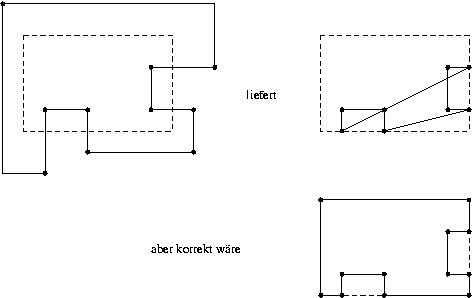
Der Sutherland & Hodgman-Algorithmus clippt an vier Fensterkanten nacheinander:
fuer jede Clipping-Gerade E tue:
fuer jeden Polygonpunkt P tue:
falls P sichtbar: uebernimm ihn
falls Kante von P zu seinem Nachfolger E schneidet:
uebernimm den Schnittpunkt
/********************************************************************************/
/* */
/* Clippen von Polygonen an einem Fenster nach Sutherland-Hodgmann */
/* */
/********************************************************************************/
public boolean on_Visible_Side( // Liefert true, wenn der Punkt p
Point p, // bzgl. der waage- oder senkrechten
int value, // Kante beim entspr. y- oder x-Wert
int edge) { // value auf der sichtb. Seite liegt.
// edge symbolisiert die Lage der
// Kante analog zum Regioncode.
switch (edge) {
case LEFT : return p.x >= value; // linke Fenster-Kante
case RIGHT : return p.x <= value; // rechte Fenster-Kante
case TOP : return p.y >= value; // obere Fenster-Kante
case BOTTOM : return p.y <= value; // untere Fenster-Kante
}
return false; // sonst: draussen
}
private Point intersection( // liefert true, falls sich die Linie
Point p1, Point p2, // p1-p2 mit waage- oder senkrechter
int value, // Clipping-Kante bei y- oder x-Wert
int edge) { // value schneidet. edge ist die
// Clipping Kante relativ zum
// Clipping-Rechteck
boolean p1_vis, p2_vis; // true, falls p1 bzw p2 sichtbar
double slope; // Steigung der Geraden p1-p2
// y = (x-p1.x)*slope + p1.y
Point i = null; // liefert den Schnittpunkt i zurueck
p1_vis=on_Visible_Side(p1,value,edge); // p1 sichtbar ?
p2_vis=on_Visible_Side(p2,value,edge); // p2 sichtbar ?
if ((p1_vis && p2_vis) || (!p1_vis && !p2_vis))
return i; // kein Schnittpkt
else {
slope = (double)(p2.y-p1.y) / (double) (p2.x-p1.x); // Steigung
if (edge==TOP || edge == BOTTOM) { // waagerechte Kante
i.x = (int)((value-p1.y) / slope) + p1.x;
i.y = value;
}
else { // senkrechte Kante
i.x = value;
i.y = (int)((value-p1.x) * slope) + p1.y;
}
return i; // Schnittpunkt liefern
}
}
private boolean sutherland_hodgeman(Vector pv, int value, int edge) {
int old; // durchlaeuft die alten Punkte
Vector hilf = new Vector(pv.size(), 1); // Hilfsvektor
Point s, i;
for (old = 0; old < pv.size() - 1; old++) {
s = (Point) pv.elementAt(old);
if (on_Visible_Side(s, value, edge)) {
hilf.addElement(s);
}
i = l.intersects(s, pv.elemenatAt(old+1), value, edge);
if (i != null) {
hilf.addElement(i);
}
}
if (hilf.size() > 0) { // Falls Punkte gemerkt
hilf.addElement(hilf.elementAt(0)); // 1. nochmal ans Ende
}
pv = hilf; // neuen Vektor merken
return hilf.size() != 0; // wenn draussen: Vektor leer
}