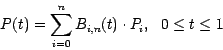
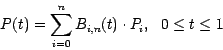
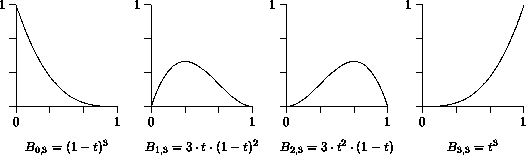
Die wichtigsten Eigenschaften der Bernsteinpolynome:
Da alle Bernsteinpolynome für ![]() ungleich
Null sind, beeinflussen alle Stützpunkte in diesem Intervall den
Kurvenverlauf.
ungleich
Null sind, beeinflussen alle Stützpunkte in diesem Intervall den
Kurvenverlauf.
Die Kurve beginnt im Stützpunkt ![]() tangential
zur Geraden
tangential
zur Geraden
![]() , endet im Stützpunkt
, endet im Stützpunkt
![]() tangential zur Geraden
tangential zur Geraden
![]() und verläuft innerhalb der konvexen Hülle der Stützpunkte.
Somit können mehrere Bézier-Kurven aneinandergesetzt werden
durch Identifikation von Endpunkt und Anfangspunkt aufeinanderfolgender
Bézierkurven.
Einen stetig differenzierbaren Übergang erreicht man bei Kollinearität
der Punkte
und verläuft innerhalb der konvexen Hülle der Stützpunkte.
Somit können mehrere Bézier-Kurven aneinandergesetzt werden
durch Identifikation von Endpunkt und Anfangspunkt aufeinanderfolgender
Bézierkurven.
Einen stetig differenzierbaren Übergang erreicht man bei Kollinearität
der Punkte
![]() .
.
Berechnung der Bézier-Kurve nach de Casteljau
Um die aufwendige Auswertung der Bernsteinpolynome zu vermeiden, wurde von de Casteljau ein Iterationsverfahren vorgeschlagen, welches durch fortgesetztes Zerteilen von Linien den gewünschten Kurvenpunkt approximieren kann.
Es gilt:
wobei die tiefgestellten Indizes angeben, welche Stützpunkte in die
Berechnung einfließen.
D.h.
eine Bézier-Kurve vom Grad ![]() läßt sich
durch zwei
Bézier-Kurven vom Grad
läßt sich
durch zwei
Bézier-Kurven vom Grad ![]() definieren, indem
für ein festes
definieren, indem
für ein festes ![]() die Punkte beider Kurven berechnet werden, und
die Verbindungsstrecke im Verhältnis
die Punkte beider Kurven berechnet werden, und
die Verbindungsstrecke im Verhältnis ![]() geteilt wird.
geteilt wird.
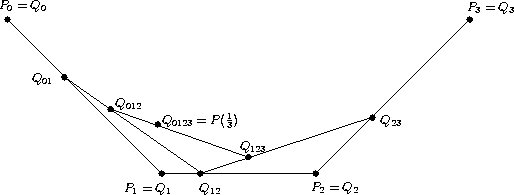
Abbildung
7.3
zeigt die Berechnung
eines Kurvenpunktes für
![]() .
Die Indizes geben an, welche Stützpunkte beteiligt sind.
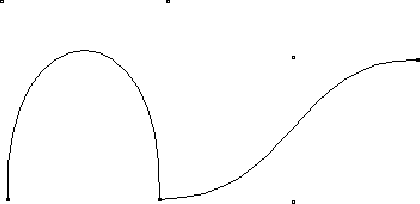
Abbildung
7.4
zeigt das Ergebnis dieser
Iteration für zwei aneinanderliegende kubische
Bézierkurven (Rekursionstiefe 3).
.
Die Indizes geben an, welche Stützpunkte beteiligt sind.
Abbildung
7.4
zeigt das Ergebnis dieser
Iteration für zwei aneinanderliegende kubische
Bézierkurven (Rekursionstiefe 3).
/**************************************************************************/
/* */
/* Zeichnen einer Bezierkurve 3. Grades nach De Casteljau */
/* */
/**************************************************************************/
private void bezier(
double px0, double py0, // mit Stuetzpunkt p0
double px1, double py1, // mit Stuetzpunkt p1
double px2, double py2, // mit Stuetzpunkt p2
double px3, double py3, // mit Stuetzpunkt p3
int depth) // aktuelle Rekursionstiefe
{
double qx01,qy01,qx12,qy12,qx23,qy23, // Hilfspunkte
qx012,qy012,qx123,qy123,qx0123,qy0123;
if (depth == 0) // Iterationstiefe erreicht
drawLine(new Point( (int)px0, (int)py0), // Linie zeichnen
new Point( (int)px3, (int)py3));
else {
depth--;
qx01 = (px0+px1)/2; qy01 = (py0+py1)/2;
qx12 = (px1+px2)/2; qy12 = (py1+py2)/2;
qx23 = (px2+px3)/2; qy23 = (py2+py3)/2;
qx012 = (qx01+qx12)/2; qy012 = (qy01+qy12)/2;
qx123 = (qx12+qx23)/2; qy123 = (qy12+qy23)/2;
qx0123 = (qx012+qx123)/2; qy0123 = (qy012+qy123)/2;
bezier(px0,py0,qx01,qy01,qx012,qy012,qx0123,qy0123,depth);
bezier(qx0123,qy0123,qx123,qy123,qx23,qy23,px3,py3,depth);
}
}
|