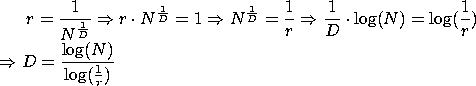Ein selbstähnliches Objekt hat 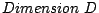 ,
falls es in
,
falls es in 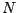 identische Kopien unterteilt werden kann, die
jeweils skaliert sind mit dem Faktor
identische Kopien unterteilt werden kann, die
jeweils skaliert sind mit dem Faktor
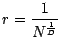 .
.
- Beispiel:
- Linie hat Dimension
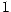 , denn sie besteht aus
, denn sie besteht aus 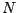 Stücken der
Größe
Stücken der
Größe 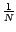 .
.
Quadratische Fläche hat Dimension 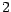 , denn sie besteht aus
, denn sie besteht aus 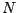 Flächen der Größe
Flächen der Größe
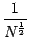 ,
,
z.B. 9 Teilflächen mit Kantenlängen skaliert um
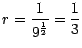
Sind 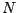 und
und 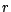 bekannt, läßt sich
bekannt, läßt sich 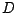 bestimmen:
bestimmen:
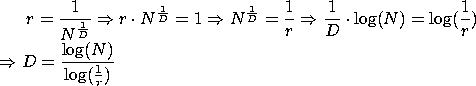
- Beispiel:
- Die Koch'sche Schneeflocke hat Dimension
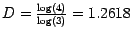 ,
denn jeder Kantenzug besteht aus
,
denn jeder Kantenzug besteht aus 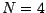 Kopien,
jeweils skaliert um den Faktor
Kopien,
jeweils skaliert um den Faktor 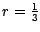 .
.




![]() ,
falls es in
,
falls es in ![]() identische Kopien unterteilt werden kann, die
jeweils skaliert sind mit dem Faktor
identische Kopien unterteilt werden kann, die
jeweils skaliert sind mit dem Faktor
![]() .
.
![]() und
und ![]() bekannt, läßt sich
bekannt, läßt sich ![]() bestimmen:
bestimmen: