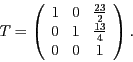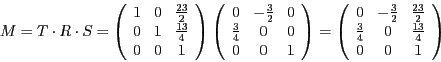Aufgabe 2.1 (20 Punkte)
Seien die Dreiecke 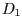 durch die Eckpunkte
durch die Eckpunkte
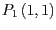 ,
,
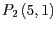 und
und
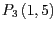 und
und 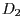 durch die Eckpunkte
durch die Eckpunkte
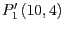 ,
,
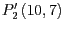 und
und
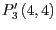 gegeben.
gegeben.
- Zeichnen Sie die Dreiecke
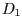 und
und 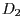 .
.
- Geben Sie Transformationen
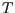 ,
, 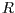 und
und 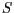 an, sodass
an, sodass
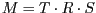 den Punkt
den Punkt 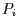 in den Punkt
in den Punkt
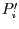 für
für
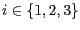 überführt. Hierbei soll
überführt. Hierbei soll 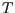 eine Translation,
eine Translation, 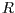 eine Rotation
und
eine Rotation
und 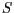 eine Skalierung sein.
eine Skalierung sein.
- Stellen Sie die Matrix
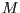 auf und zeigen Sie durch Nachrechnen,
dass sie die Voraussetzungen erfüllt.
auf und zeigen Sie durch Nachrechnen,
dass sie die Voraussetzungen erfüllt.
Musterlösung vom 09.05.2012:
- aufgabe21ausgangslage
- Aus der Zeichnung wird deutlich, dass
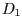 um
um 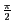 gegen den Uhrzeigersinn (CCW) gedreht werden muss. Die vorher durchgeführte
Skalierung muss darauf Rücksicht nehmen. Die Ausdehnung von
gegen den Uhrzeigersinn (CCW) gedreht werden muss. Die vorher durchgeführte
Skalierung muss darauf Rücksicht nehmen. Die Ausdehnung von 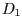 ist jeweils 4 Einheiten in
ist jeweils 4 Einheiten in 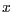 - und
- und 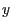 -Richtung. Die Ausdehnung
von
-Richtung. Die Ausdehnung
von 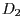 ist 6 in
ist 6 in 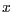 - und 3 in
- und 3 in 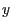 -Richtung. Es ergibt sich
die Skalierungsmatrix
-Richtung. Es ergibt sich
die Skalierungsmatrix
Die Rotationsmatrix 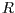 hat wegen
hat wegen
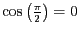 und
und
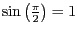 die Gestalt
die Gestalt
Mit diesen beiden Transformationen hat das Dreieck die gewünschte
Form. Um es an die richtige Stelle zu verschieben, berechnen wir zunächst
mit Hilfe von 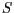 und
und 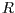 den transformierten Punkt
den transformierten Punkt 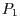 (für
die Matrixmultiplikation wird
(für
die Matrixmultiplikation wird 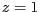 ergänzt).
ergänzt).
Um
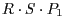 in den Punkt
in den Punkt 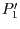 zu verschieben, müssen
wir also
zu verschieben, müssen
wir also
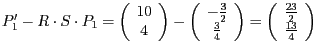 als Translationsvektor nehmen. Wir erhalten für die Translationsmatrix
also
als Translationsvektor nehmen. Wir erhalten für die Translationsmatrix
also
- Die Gesamtmatrix ist




![]() durch die Eckpunkte
durch die Eckpunkte
![]() ,
,
![]() und
und
![]() und
und ![]() durch die Eckpunkte
durch die Eckpunkte
![]() ,
,
![]() und
und
![]() gegeben.
gegeben.
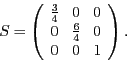
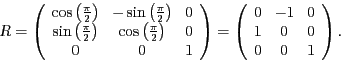
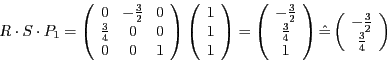
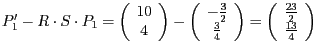 als Translationsvektor nehmen. Wir erhalten für die Translationsmatrix
also
als Translationsvektor nehmen. Wir erhalten für die Translationsmatrix
also