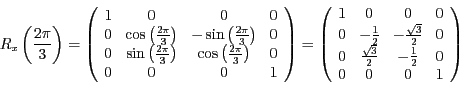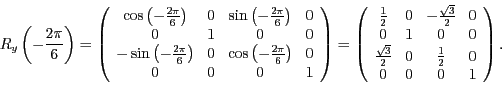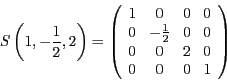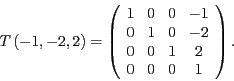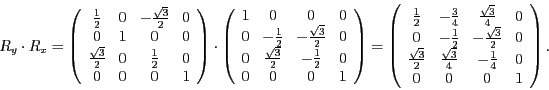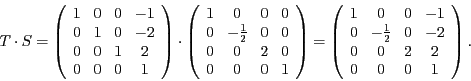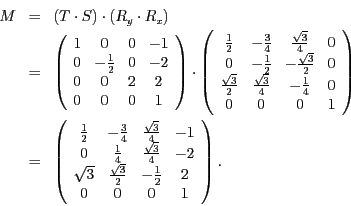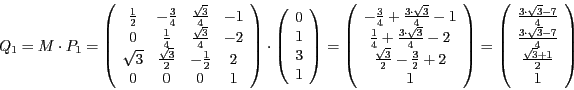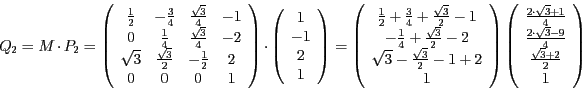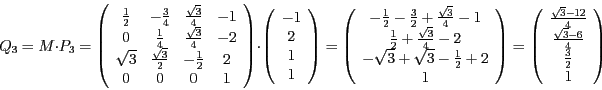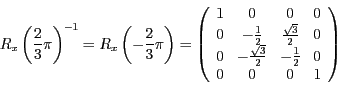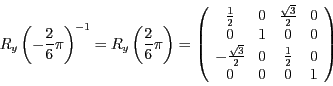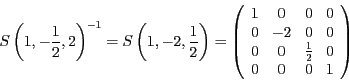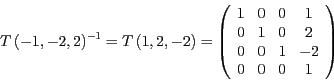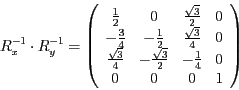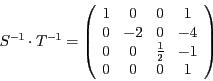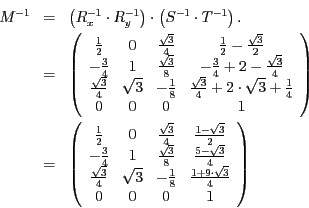Aufgabe 2.3 (40 Punkte)
Sei das Dreieck 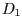 durch die Punkte
durch die Punkte
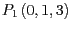 ,
,
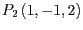 und
und
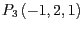 und die
folgenden Transformationen in
und die
folgenden Transformationen in
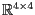 gegeben.
gegeben.
- Rotation
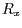 um
um
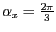 um die
um die 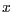 -Achse,
-Achse,
- Rotation
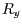 um
um
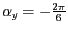 um die
um die 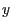 -Achse,
-Achse,
- Skalierung
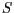 um den Faktor
um den Faktor
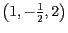 und
und
- Translation
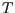 um den Vektor
um den Vektor
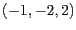 .
.
- Stellen Sie die einzelnen Transformationsmatrizen exakt auf und berechnen
Sie das Produkt
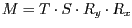 ebenfalls exakt.
ebenfalls exakt.
- Berechnen Sie das Dreieck
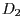 , welches durch das Anwenden der
Gesamttransformation
, welches durch das Anwenden der
Gesamttransformation 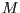 auf das Dreieck
auf das Dreieck 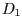 entsteht.
entsteht.
- Berechnen Sie die inverse Transformation
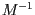 zu
zu 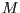 exakt.
exakt.
- Erweitern Sie das Projekt aus Aufgabe 2 und schreiben Sie eine Javaklasse
Transformation, in deren main-Methode das Dreieck
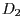 mithilfe der Klassen Vector4f und Matrix4f
aus dem Package org.lwjgl.util.vector berechnet wird.
mithilfe der Klassen Vector4f und Matrix4f
aus dem Package org.lwjgl.util.vector berechnet wird.
Musterlösung vom 09.05.2012:
- Für die Rotationen ergeben sich die Matrizen
und
Für die Skalierung S und die Translation T ergeben sich die Matrizen
und
Die Multiplikation der beiden Rotationen ergibt
Die Multiplikation der Translation mit der Skalierung ergibt
Und somit ist die gesamte Transformation
- Um das Dreieck
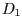 in das transformierte Dreieck zu überführen,
müssen die einzelnen Punkte mit der Matrix M multipliziert werden.
Um die Multiplikation ausführen zu können, müssen die Vektoren natürlich
um die homogene Koordinate
in das transformierte Dreieck zu überführen,
müssen die einzelnen Punkte mit der Matrix M multipliziert werden.
Um die Multiplikation ausführen zu können, müssen die Vektoren natürlich
um die homogene Koordinate 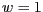 erweitert werden.
erweitert werden.
Das Dreieck 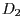 setzt sich dann aus den Punkten
setzt sich dann aus den Punkten 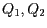 und
und 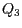 zusammen.
zusammen.
- Um die Transformation
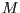 zu invertieren, werden ihre Bestandteile
jeweils invertiert und dann in umgekehrter Reihenfolge zusammengefügt.
zu invertieren, werden ihre Bestandteile
jeweils invertiert und dann in umgekehrter Reihenfolge zusammengefügt.
Und damit erhalten wir schließlich die Gesamttransformation
/home/cg/2012/Uebung/Blatt2/Aufg/Transformation.java



![]() durch die Punkte
durch die Punkte
![]() ,
,
![]() und
und
![]() und die
folgenden Transformationen in
und die
folgenden Transformationen in
![]() gegeben.
gegeben.