Effizienz des RSA-Verfahrens

Die Effizienz stützt sich auf folgende Überlegungen:

a)

Potenziere mod n
Nicht e -mal mit x malnehmen, denn Aufwand wäre O(2⁵⁰⁰) , sondern:

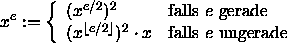
Aufwand: O (log e) , d.h. proportional zur Anzahl der Dezimalstellen.

b)

Bestimme e : = d^{- 1}

Algorithmus von Euklid zur Bestimmung des ggt :

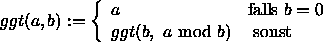
Bestimme ggt( $\varphi$ (n), d ) und stelle den auftretenden Rest als Linearkombination von $\varphi$ (n) und d dar.

Beispiel:

c)

Konstruktion einer großen Primzahl

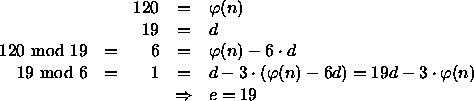
Wähle 500 Bit lange ungerade Zahl x .

Teste, ob x, x + 2, x + 4, x + 6,... Primzahl ist.

Sei $\Pi$ (x) die Anzahl der Primzahlen unterhalb von x . Es gilt:
$\Pi$ (x) $\approx$ ${\frac{x}{\ln x}}$ $\Rightarrow$ Dichte $\approx$ ${\frac{1}{\ln x}}$ $\Rightarrow$ mittlerer Abstand $\approx$ ln x

Also zeigt sich Erfolg beim Testen ungerader Zahlen der Größe n = 2⁵⁰⁰ nach etwa ${\frac{\ln 2^{500}}{4}}$ = 86 Versuchen.

Komplexitätsklassen für die Erkennung von Primzahlen:

L $\in$ $\mathbb {RP}$ : $\iff$ es gibt Algorithmus A , der angesetzt auf die Frage, ob x $\in$ L , nach polynomialer Zeit mit ja oder nein anhält und folgende Gewähr für die Antwort gilt:

Antwort: ja $\Rightarrow$ x ist zusammengesetzt.

Antwort: nein $\Rightarrow$ x ist höchstwahrscheinlich prim.

Bei 50 Versuchen $\Rightarrow$ Fehler $\le$ $\varepsilon^{50}_{}$ .

Satz von Rabin:

Sei n = 2^k · q + 1 eine Primzahl, x < n

1): x^q $\equiv$ 1 mod n oder
2): x^{q · 2ⁱ} $\equiv$ - 1 mod n für ein i $\in$ {0, ..., k - 1}

Beispiel:

Sei n = 97 = 2⁵ · 3 + 1 , sei x = 2.

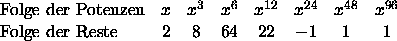
Definition eines Zeugen:

Sei n = 2^k · q + 1 .

Eine Zahl x < n heißt Zeuge für die Zusammengesetztheit von n

1): ggt(x,n) $\neq$ 1 oder
2): x^q $\not\equiv$ 1 mod n und x^{q · 2ⁱ} $\not\equiv$ - 1 für alle i $\in$ {0,...,k - 1}

Satz von Rabin:

Ist n zusammengesetzt, so gibt es mindestens ${\frac{3}{4}}$ n Zeugen.

function prob-prim (n: integer): boolean
z:=0;
repeat
    z=z+1;
    wuerfel x; 
until (x ist Zeuge fuer n) OR (z=50);
return (z=50)

Fehler: ( ${\frac{1}{4}}$ )⁵⁰ $\sim$ 10^{- 30}