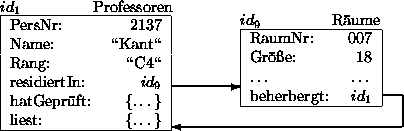
Eine 1 : 1 -Beziehung wird symmetrisch in beiden beteiligten Objekt-Typen modelliert:
class Professoren {
attribute long PersNr;
...
relationship Raeume residiertIn;
};
class Raeume {
attribute long RaumNr;
attribute short Groesse;
...
relationship Professoren beherbergt;
};
Abbildung 15.4 zeigt eine mögliche Ausprägung der Beziehungen residiertIn und beherbergt.
Allerdings wird durch die gegebene Klassenspezifikation weder die Symmetrie noch die 1:1-Einschränkung garantiert. Abbildung 15.5 zeigt einen inkonsistenten Zustand des Beziehungspaars residiertIn und beherbergt.
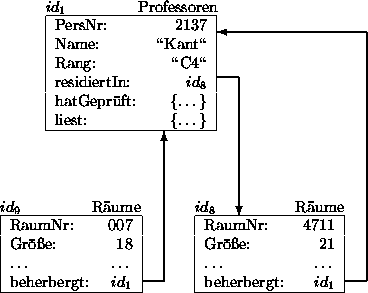
Um Inkonsistenzen dieser Art zu vermeiden, wurde im ODMG-Objektmodell das inverse-Konstrukt integriert:
class Professoren {
attribute long PersNr;
...
relationship Raeume residiertIn inverse Raeume::beherbergt;
};
class Raeume {
attribute long RaumNr;
attribute short Groesse;
...
relationship Professoren beherbergt inverse Professoren::residiertIn;
};
Damit wird sichergestellt, daß immer gilt:
p = r.beherbergt ![]() r = p.residiertIn
r = p.residiertIn
Binäre 1:N - Beziehungen werden modelliert mit Hilfe des Mengenkonstruktors set, der im nächsten Beispiel einem Professor eine Menge von Referenzen auf Vorlesungen-Objekte zuordnet:
class Professoren {
...
relationship set (Vorlesungen) liest inverse Vorlesungen::gelesenVon;
};
class Vorlesungen {
...
relationship Professoren gelesenVon inverse Professoren::liest;
};
Man beachte, daß im relationalen Modell die
Einführung eines Attributs liest
im Entity-Typ Professoren
die Verletzung der 3. Normalform verursacht hätte.
Binäre N:M - Beziehungen werden unter Verwendung von zwei set-Konstruktoren modelliert:
class Studenten {
...
relationship set (Vorlesungen) hoert inverse Vorlesungen::Hoerer;
};
class Vorlesungen {
...
relationship set (Studenten) Hoerer inverse Studenten::hoert;
};
Durch die inverse-Spezifikation wird sichergestellt, daß gilt:
s ![]() v.Hoerer
v.Hoerer ![]() v
v ![]() s.hoert
s.hoert
Analog lassen sich rekursive N : M - Beziehungen beschreiben:
class Vorlesungen {
...
relationship set (Vorlesungn) Vorgaenger inverse Vorlesungen::Nachfolger;
relationship set (Vorlesungn) Nachfolger inverse Vorlesungen::Vorgaenger;
};
Ternäre oder n![]() 3 stellige Beziehungen benötigen
einen eigenständigen Objekttyp, der die Beziehung repräsentiert.
Zum Beispiel wird die ternäre Beziehung
3 stellige Beziehungen benötigen
einen eigenständigen Objekttyp, der die Beziehung repräsentiert.
Zum Beispiel wird die ternäre Beziehung
| pruefen | : | {[ MatrNr, VorlNr, PersNr, Note ]} |
class Pruefungen {
attribute float Note;
relationship Professoren Pruefer inverse Professoren::hatgeprueft;
relationship Studenten Pruefling inverse Studenten::wurdegeprueft;
relationship Vorlesungen Inhalt inverse Vorlesungen::wurdeAbgeprueft;
};
class Professoren {
attribute long PersNr;
attribute string Name;
attribute string Rang;
relationship Raeume residiertIn inverse Raeume::beherbergt;
relationship set(Vorlesungen) liest inverse Vorlesungen::gelesenVon;
relationship set(Pruefungen) hatgeprueft inverse Pruefungen::Pruefer;
};
class Vorlesungen {
attribute long VorlNr;
attribute string Titel;
attribute short SWS;
relationship Professoren gelesenVon inverse Professoren::liest;
relationship set(Studenten) Hoerer inverse Studenten::hoert;
relationship set(Vorlesungen) Nachfolger inverse Vorlesungen::Vorgaenger;
relationship set(Vorlesungen) Vorgaenger inverse Vorlesungen::Nachfolger;
relationship set(Pruefungen) wurdeAbgeprueft inverse Pruefungen::Inhalt;
};
class Studenten {
attribute long MatrNr;
attribute string Name;
attribute short Semester;
relationship set(Pruefungen) wurdeGeprueft inverse Pruefungen::Pruefling;
relationship set(Vorlesungen) hoert inverse Vorlesungen::Hoerer;
};
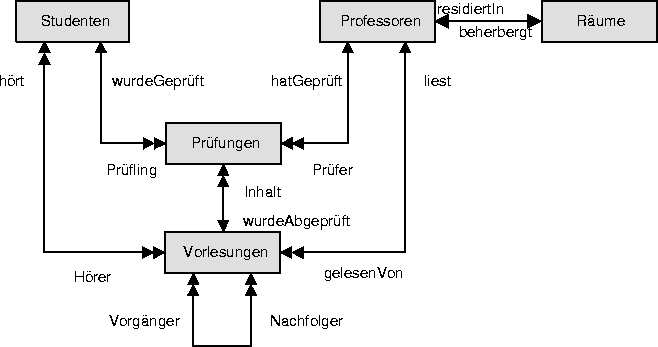
Abbildung 15.6 visualisiert die bislang eingeführten Beziehungen.
Die Anzahl der Pfeilspitzen gibt die Wertigkeit der Beziehung an:
|
|
bezeichnet eine 1 : 1 -Beziehung |
|
bezeichnet eine 1 : N -Beziehung |
|
|
bezeichnet eine N : 1 -Beziehung |
|
bezeichnet eine N : M -Beziehung |