B*-Baum

Betrachten wir das Index-File als Daten-File, so können wir dazu ebenfalls einen weiteren Index konstruieren und für dieses File wiederum einen Index usw. Diese Idee führt zum B*-Baum.

Ein B*-Baum mit Parameter k wird charakterisiert durch folgende Eigenschaften:

Jeder Weg von der Wurzel zu einem Blatt hat dieselbe Länge.
Jeder Knoten außer der Wurzel und den Blättern hat mindestens k Nachfolger.
Jeder Knoten hat höchstens 2 · k Nachfolger.
Die Wurzel hat keinen oder mindestens 2 Nachfolger.

Der Baum T befindet sich im Hintergrundspeicher, und zwar nimmt jeder Knoten einen Block ein. Ein Knoten mit j Nachfolgern speichert j Paare von Schlüsseln und Adressen (s₁, a₁),...,(s_j, a_j) . Es gilt s₁ $\leq$ s₂ $\leq$ .. $\leq$ s_j . Eine Adresse in einem Blattknoten bezeichnet den Datenblock mit den restlichen Informationen zum zugehörigen Schlüssel, sonst bezeichnet sie den Block zu einem Baumknoten: Enthalte der Block für Knoten p die Einträge (s₁,a₁),...,(s_j,a_j) . Dann ist der erste Schlüssel im i-ten Sohn von p gleich s_i , alle weiteren Schlüssel in diesem Sohn (sofern vorhanden) sind größer als s_i und kleiner als s_{i + 1} .

Wir betrachten nur die Operationen auf den Knoten des Baumes und nicht auf den eigentlichen Datenblöcken. Gegeben sei der Schlüssel s .

LOOKUP:: Beginnend bei der Wurzel steigt man den Baum hinab in Richtung des Blattes, welches den Schlüssel s enthalten müßte. Hierzu wird bei einem Knoten mit Schlüsseln s₁,s₂,...,s_j als nächstes der i-te Sohn besucht, wenn gilt s_i $\leq$ s < s_{i + 1} .
MODIFY:: Wenn das Schlüsselfeld verändert wird, muß ein DELETE mit nachfolgendem INSERT erfolgen. Wenn das Schlüsselfeld nicht verändert wird, kann der Datensatz nach einem LOOKUP überschrieben werden.
INSERT:: Nach LOOKUP sei Blatt B gefunden, welches den Schlüssel s enthalten soll. Wenn B weniger als 2k Einträge hat, so wird s eingefügt, und es werden die Vorgängerknoten berichtigt, sofern s kleinster Schlüssel im Baum ist. Wenn B 2 · k Einträge hat, wird ein neues Blatt B' generiert, mit den größeren k Einträgen von B gefüllt und dann der Schlüssel s eingetragen. Der Vorgänger von B und B' wird um einen weiteren Schlüssel s' (kleinster Eintrag in B' ) erweitert. Falls dabei Überlauf eintritt, pflanzt sich dieser nach oben fort.
DELETE:: Nach LOOKUP sei Blatt B gefunden, welches den Schlüssel s enthält. Das Paar (s,a) wird entfernt und ggf. der Schlüsseleintrag der Vorgänger korrigiert. Falls B jetzt k - 1 Einträge hat, wird der unmittelbare Bruder B' mit den meisten Einträgen bestimmt. Haben beide Brüder gleich viel Einträge, so wird der linke genommen. Hat B' mehr als k Einträge, so werden die Einträge von B und B' auf diese beiden Knoten gleichmäßig verteilt. Haben B und B' zusammen eine ungerade Anzahl, so erhält der linke einen Eintrag mehr. Hat B' genau k Einträge, so werden B und B' verschmolzen. Die Vorgängerknoten müssen korrigiert werden.

Abbildung 4.11 zeigt das dynamische Verhalten eines B*-Baums mit dem Parameter k = 2 . Es werden nacheinander die Schlüssel 3, 7, 1, 16, 4, 14, 12, 6, 2, 15, 13, 8, 10, 5, 11, 9 eingefügt und insgesamt 8 Schnappschüsse gezeichnet.

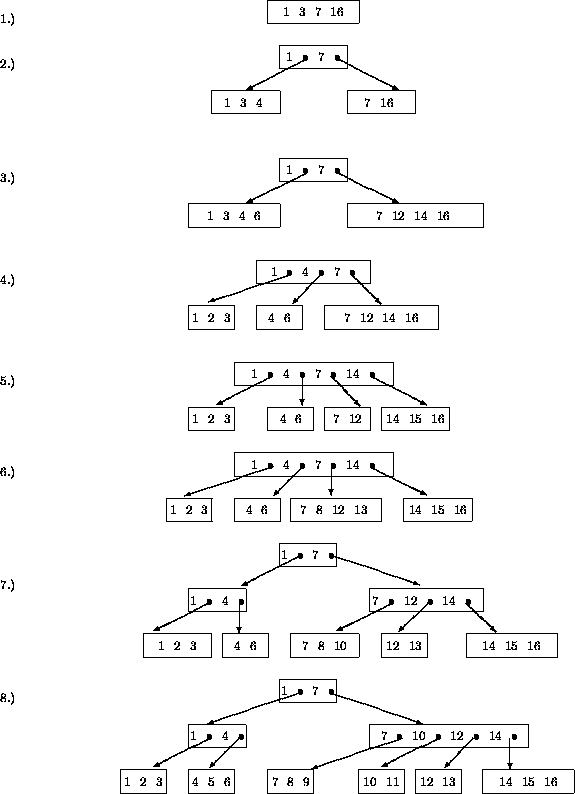
dynamisches Verhalten eines B*-Baums

Der Parameter k ergibt sich aus dem Platzbedarf für die Schlüssel/Adreßpaare und der Blockgröße. Die Höhe des Baumes ergibt sich aus der benötigten Anzahl von Verzweigungen, um in den Blättern genügend Zeiger auf die Datenblöcke zu haben.

Beispiel

für die Berechnung des Platzbedarfs eines B*-Baums:
Gegeben seien 300.000 Datenrecords à 100 Bytes. Jeder Block umfasse 1.024 Bytes. Ein Schlüssel sei 15 Bytes lang, eine Adresse bestehe aus 4 Bytes. Daraus errechnet sich der Parameter k wie folgt

$\displaystyle\lfloor$ $\displaystyle{\textstyle\frac{1024}{15 + 4}}$ $\displaystyle\rfloor$ = 53 $\displaystyle\Rightarrow$ k = 26

Die Wurzel sei im Mittel zu 50 % gefüllt (hat also 26 Söhne), ein innerer Knoten sei im Mittel zu 75 % gefüllt (hat also 39 Söhne), ein Datenblock sei im Mittel zu 75 % gefüllt (enthält also 7 bis 8 Datenrecords). 300.000 Records sind also auf $\lfloor$ ${\frac{300.000}{7,5}}$ $\rfloor$ = 40.000 Datenblöcke verteilt.

Die Zahl der Zeiger entwickelt sich daher auf den oberen Ebenen des Baums wie folgt:

Höhe	Anzahl Knoten	Anzahl Zeiger
0	1	26
1	26	26 · 39	=	1.014
2	26 · 39	26 · 39 · 39	=	39.546

Damit reicht die Höhe 2 aus, um genügend Zeiger auf die Datenblöcke bereitzustellen. Der Platzbedarf beträgt daher

1 + 26 + 26 · 39 + 39546 $\displaystyle\approx$ 40.000Blöcke.

Das LOOKUP auf ein Datenrecord verursacht also vier Blockzugriffe: es werden drei Indexblöcke auf Ebene 0, 1 und 2 sowie ein Datenblock referiert. Zum Vergleich: Das Heapfile benötigt 30.000 Blöcke.

Soll für offenes Hashing eine mittlere Zugriffszeit von 4 Blockzugriffen gelten, so müssen in jedem Bucket etwa 5 Blöcke sein (1 Zugriff für Hash-Directory, 3 Zugriffe im Mittel für eine Liste von 5 Blöcken). Von diesen 5 Blöcken sind 4 voll, der letzte halbvoll. Da 10 Records in einen Datenblock passen, befinden sich in einem Bucket etwa 4,5 · 10 = 45 Records. Also sind ${\frac{300.000}{45}}$ = 6.666 Buckets erforderlich. Da 256 Adressen in einen Block passen, werden $\lfloor$ ${\frac{6666}{256}}$ $\rfloor$ = 26 Directory-Blöcke benötigt. Der Platzbedarf beträgt daher 26 + 5 · 6666 = 33356 .

Zur Bewertung von B*-Bäumen läßt sich sagen:

Vorteile: dynamisch, schnell, Sortierung generierbar (ggf. Blätter verzeigern).
Nachteile: komplizierte Operationen, Speicheroverhead.