k-d-Baum

Durch die Datenpunkte A,B,C,D,E,F,G,H partitionierte Fläche

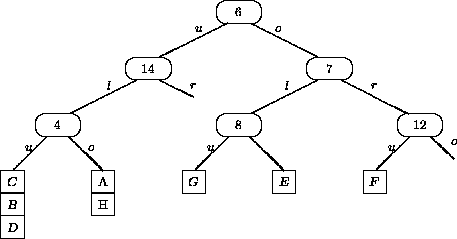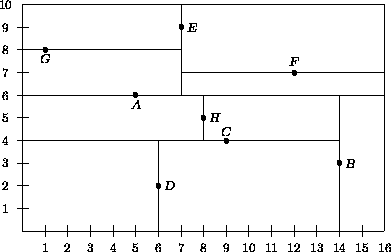
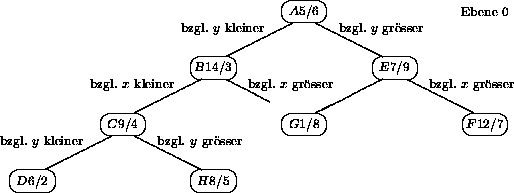
Eine Verallgemeinerung eines binären Suchbaums mit einem Sortierschlüssel bildet der k-d-Baum mit k-dimensionalem Sortierschlüssel. Er verwaltet eine Menge von mehrdimensionalen Datenpunkten, wie z.B. Abbildung 5.2 für den 2-dimensionalen Fall zeigt. In der homogenen Variante enthält jeder Baumknoten ein komplettes Datenrecord und zwei Zeiger auf den linken und rechten Sohn (Abbildung 5.3). In der inhomogenen Variante enhält jeder Baumknoten nur einen Schlüssel und die Blätter verweisen auf die Datenrecords (Abbildung 5.4). In beiden Fällen werden die Werte der einzelnen Attribute abwechselnd auf jeder Ebene des Baumes zur Diskriminierung verwendet. Es handelt sich um eine statische Struktur; die Operationen Löschen und die Durchführung einer Balancierung sind sehr aufwendig.

2-d-Baum (homogen) zu den Datenpunkten A,B,C,D,E,F,G,H

Im 2-dimensionalen Fall gilt für jeden Knoten mit Schlüssel [x/y] :

im linken Sohn im rechten Sohn

$$\leq$$ auf ungerader Ebene alle Schlüssel > x

$$\leq$$ auf gerader Ebene alle Schlüssel > y

Die Operationen auf einem 2 - d -Baum laufen analog zum binärem Baum ab:

• Insert:
  Suche mit Schlüssel [x/y] unter Abwechslung der Dimension die Stelle, wo der [x/y] -Knoten sein müßte und hänge ihn dort ein.
• Exakt Match (z.B. finde Record [ 15/5 ]):
  Suche mit Schlüssel [ x/y ] unter Abwechslung der Dimension bis zu der Stelle, wo der [ x/y ]-Knoten sein müßte.
• Partial Match (z.B. finde alle Records mit x = 7 ):
  An den Knoten, an denen nicht bzgl. x diskriminiert wird, steige in beide Söhne ab; an den Knoten, an denen bzgl. x diskriminiert wird, steige in den zutreffenden Teilbaum ab.
• Range-Query (z.B. finde alle Records [ x,y ] mit 7 $\leq$ x $\leq$ 13,5 $\leq$ y $\leq$ 8 ):
  An den Knoten, an denen die Diskriminatorlinie das Suchrechteck schneidet, steige in beide Söhne ab, sonst steige in den zutreffenden Sohn ab. Beobachtung: Laufzeit k + log n Schritte bei k Treffern!
• Best-Match (z.B. finde nächstgelegenes Record zu x = 7,y = 3 ):
  Dies entspricht einer Range-Query, wobei statt eines Suchrechtecks jetzt ein Suchkreis mit Radius gemäß Distanzfunktion vorliegt. Während der Baumtraversierung schrumpft der Suchradius. Diese Strategie ist erweiterbar auf k -best-Matches.

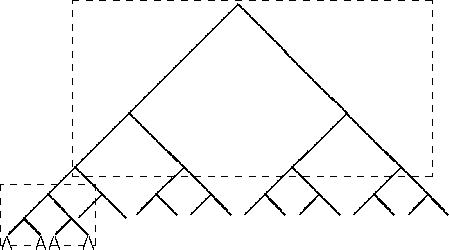
Bei der inhomogenen Variante enthalten die inneren Knoten je nach Ebene die Schlüsselinformation der zuständigen Dimension sowie Sohnzeiger auf weitere innere Knoten. Nur die Blätter verweisen auf Datenblöcke der Hauptdatei, die jeweils mehrere Datenrecords aufnehmen können. Auch die inneren Knoten werden zu Blöcken zusammengefaßt, wie auf Abbildung 5.5 zu sehen ist. In Abbildung 5.4 befinden sich z.B. die Datenrecords C, B und D in einem Block.

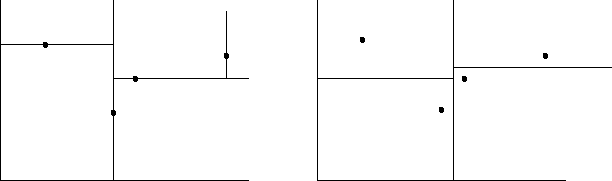
Abbildung 5.6 zeigt, daß neben der oben beschriebenen 2-d-Baum-Strategie eine weitere Möglichkeit existiert, den Datenraum zu partitionieren. Dies führt zu den sogenannten Gitterverfahren.

2-d-Baum (inhomogen) zu den Datenpunkten A,B,C,D,E,F,G,H

Zusammenfassung von je 7 inneren Knoten auf einem Index-Block

Partitionierungsmöglichkeiten des Raumes