Verwaltung geometrischer Objekte

In der bisherigen Anwendung repräsentierten die Datenpunkte im k-dimensionale Raum k -stellige Attributkombinationen. Wir wollen jetzt mithilfe der Datenpunkte geometrische Objekte darstellen und einfache geometrische Anfragen realisieren.

Intervalle A,B,C,D,E,F über der Zahlengeraden

Repräsentation von Intervallen durch Punkte

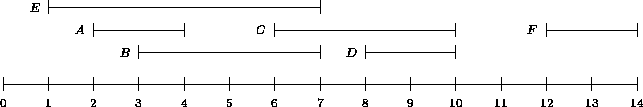
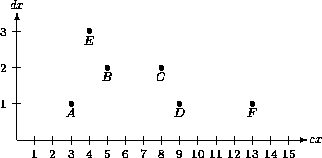
Abbildung 5.14 zeigt eine Ansammlung von Intervallen, die zu verwalten seien. Die Intervalle sollen durch Punkte im mehrdimensionalen Raum dargestellt werden. Wenn alle Intervalle durch ihre Anfangs- und Endpunkte repräsentiert würden, kämen sie auf der Datenfläche nur oberhalb der 45-Grad-Geraden zu liegen.

Abbildung 5.15 präsentiert eine wirtschaftlichere Verteilung, indem jede Gerade durch ihren Mittelpunkt und ihre halbe Länge repräsentiert wird.

Typische Queries an die Intervall-Sammlung lauten:

• Gegeben Punkt P , finde alle Intervalle, die ihn enthalten.
• Gegeben Intervall I , finde alle Intervalle, die es schneidet.

Abfragekegel zu Punkt p=5

Abbildung 5.16 zeigt den kegelförmigen Abfragebereich zum Query-Punkt p =5, in dem alle Intervalle (repräsentiert durch Punkte) liegen, die den Punkt p enthalten. Grundlage ist die Überlegung, daß ein Punkt P genau dann im Intervall mit Mitte cx und halber Länge dx enhalten ist, wenn gilt: cx - dx $\leq$ p $\leq$ cx + dx

Abfragekegel zu Intervall mit p=10 und d=1

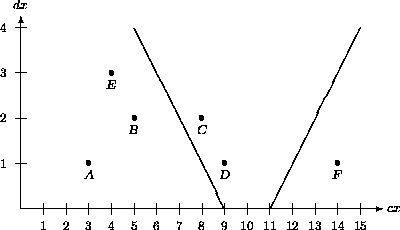
Abbildung 5.17 zeigt den kegelförmigen Abfragebereich zu dem Query-Intervall mit Mittelpunkt p =10 und halber Länge d =1, in dem alle Intervalle (repäsentiert durch Punkte) liegen, die das Query-Intervall schneiden. Grundlage ist die Überlegung, daß ein Intervall mit Mitte p und halber Länge d genau dann ein Intervall mit Mitte cx und halber Länge dx schneidet, wenn gilt: cx - dx $\leq$ p + d$\mbox{ und }$cx + dx $\geq$ p - d

Nearest-Neighbor-Suche zu Query-Punkt Q

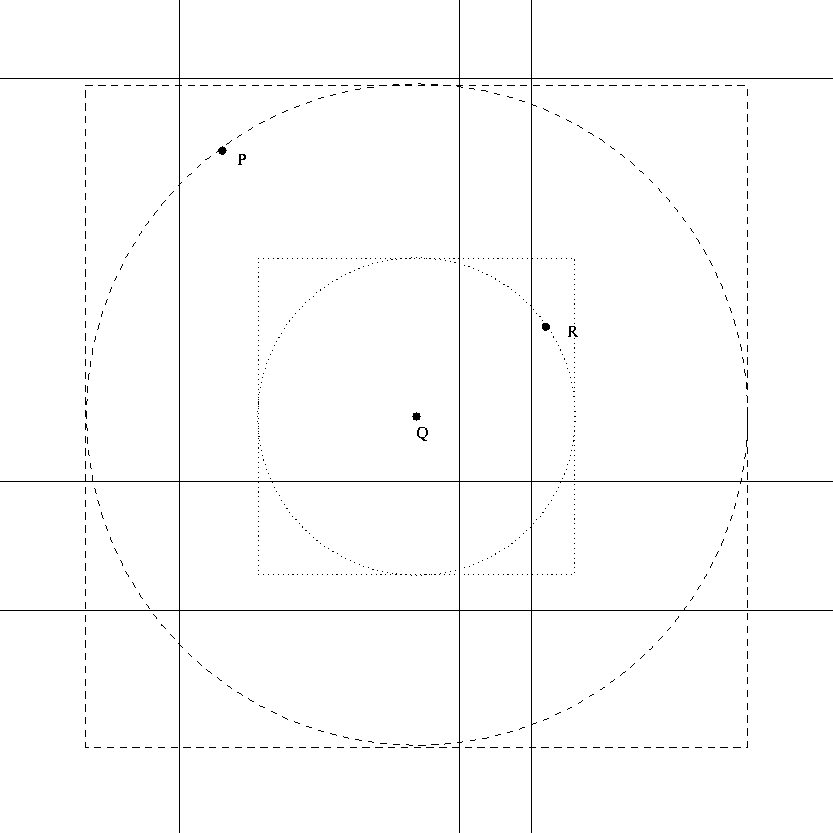
Abbildung 5.18 zeigt die Vorgehensweise bei der Bestimmung des nächstgelegenen Nachbarn (englisch: nearest neighbor). Suche zunächst auf dem Datenblock, der für den Query-Point Q zuständig ist, den nächstgelegenen Punkt P . Bilde eine Range-Query mit Quadrat um den Kreis um Q mit Radius |P - Q| . Schränke Quadratgröße weiter ein, falls nähere Punkte gefunden werden.

Die erwähnten Techniken lassen sich auf höherdimensionierte Geometrie-Objekte wie Rechtecke oder Quader erweitern. Zum Beispiel bietet sich zur Verwaltung von orthogonalen Rechtecken in der Ebene folgende Möglichkeit an: Ein Rechteck wird repräsentiert als ein Punkt im 4-dimensionalen Raum, gebildet durch die beiden 2-dimensionalen Punkte für horizontale bzw. vertikale Lage. Zu einem Query-Rechteck, bestehend aus horizontalem Intervall P und vertikalem Intervall Q , lassen sich die schneidenden Rechtecke finden im Durchschnitt der beiden kegelförmigen Abfragebereiche zu den Intervallen P und Q .