Umsetzung in ein relationales Schema

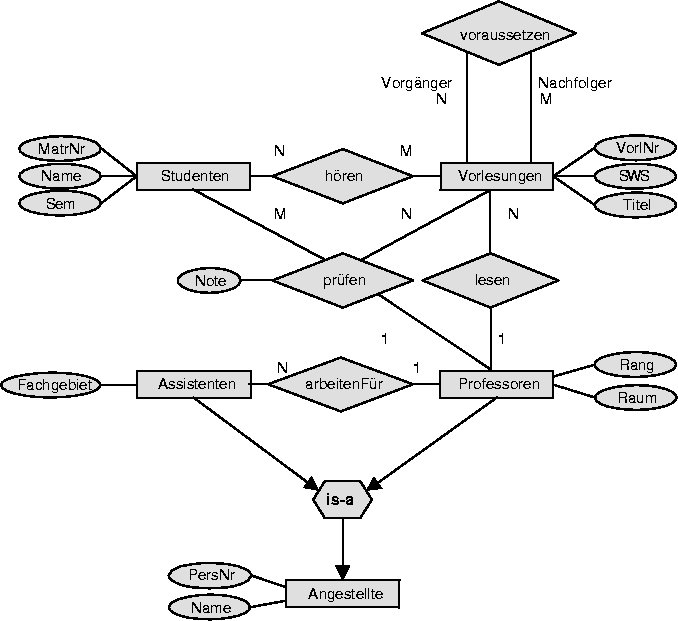
Abbildung 6.1 zeigt ein ER-Diagramm zum Universitätsbetrieb. Zunächst wollen wir die Generalisierung ignorieren, da es im relationalen Modell keine unmittelbare Umsetzung gibt. Dann verbleiben vier Entity-Typen, die auf folgende Schemata abgebildet werden:

Studenten	:	{[ MatrNr : integer, Name : string, Semester : integer] }
Vorlesungen	:	{[ VorlNr : integer, Titel : string, SWS : integer] }
Professoren	:	{[ PersNr : integer, Name : string, Rang : string, Raum : integer] }
Assistenten	:	{[ PersNr : integer, Name : string, Fachgebiet : string] }

Bei der relationalen Darstellung von Beziehungen richten wir im Initial-Entwurf für jeden Beziehungstyp eine eigene Relation ein. Später kann davon ein Teil wieder eliminiert werden. Grundsätzlich entsteht das Relationenschema durch die Folge aller Schlüssel, die an der Beziehung beteiligt sind sowie ggf. weitere Attribute der Beziehung. Dabei kann es notwendig sein, einige der Attribute umzubenennen. Die Schlüsselattribute für die referierten Entity-Typen nennt man Fremdschlüssel.

Für das Universitätsschema entstehen aus den Relationships die folgenden Schemata:

hören	:	{[ MatrNr : integer, VorlNr : integer] }
lesen	:	{[ PersNr : integer, VorlNr : integer] }
arbeitenFür	:	{[ AssiPersNr : integer, ProfPersNr : integer] }
voraussetzen	:	{[ Vorgänger : integer, Nachfolger : integer] }
prüfen	:	{[ MatrNr : integer, VorlNr : integer, PersNr : integer, Note : decimal] }

Unterstrichen sind jeweils die Schlüssel der Relation, eine minimale Menge von Attributen, deren Werte die Tupel eindeutig identifizieren.

Da die Relation hören eine N : M -Beziehung darstellt, sind sowohl die Vorlesungsnummern als auch die Matrikelnummern alleine keine Schlüssel, wohl aber ihre Kombination.

Bei der Relation lesen liegt eine 1: N -Beziehung vor, da jeder Vorlesung genau ein Dozent zugeordnet ist mit der partiellen Funktion

Also ist für die Relation lesen bereits das Attribut VorlNr ein Schlüsselkandidat, für die Relation arbeitenFür bildet die AssiPersNr einen Schlüssel.

prüfen : Studenten × Vorlesungen $\displaystyle\rightarrow$ Professoren