


- Input:
- Eine Historie H für Transaktionen
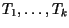 .
.
- Output:
- entweder: ,,nein, ist nicht serialisierbar`` oder ,,ja, ist serialisierbar`` +
serielles Schedule
- Idee:
- Bilde gerichteten Graph G, dessen Knoten den Transaktionen entsprechen. Für
zwei Konfliktoperationen
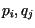 aus der Historie H mit
aus der Historie H mit 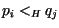 fügen wir die Kante
fügen wir die Kante
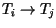 in den Graph ein.
in den Graph ein.
Es gilt das Serialisierbarkeitstheorem:
Eine Historie H ist genau dann serialisierbar, wenn der zugehörige
Serialisierbarkeitsgraph azyklisch ist. Im Falle der Kreisfreiheit läßt sich
die äquivalente serielle Historie aus der topologischen Sortierung des
Serialisierbarkeitsgraphen bestimmen.
Als Beispiel-Input für diesen Algorithmus verwenden wir die in Tabelle
13.9 gezeigte Historie über den Transaktionen 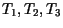 mit insgesamt 14
Operationen.
mit insgesamt 14
Operationen.
| Schritt |
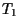 |
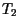 |
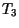 |
| 1. |
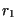 (A) (A) |
|
|
| 2. |
|
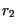 (B) (B) |
|
| 3. |
|
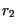 (C) (C) |
|
| 4. |
|
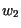 (B) (B) |
|
| 5. |
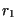 (B) (B) |
|
|
| 6. |
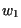 (A) (A) |
|
|
| 7. |
|
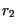 (A) (A) |
|
| 8. |
|
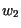 (C) (C) |
|
| 9. |
|
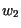 (A) (A) |
|
| 10. |
|
|
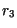 (A) (A) |
| 11. |
|
|
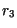 (C) (C) |
| 12. |
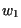 (B) (B) |
|
|
| 13. |
|
|
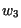 (C) (C) |
| 14. |
|
|
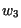 (A) (A) |
Tabelle 13.9: Historie H mit drei Transaktionen
Folgende Konfliktoperationen existieren für Historie H:
Daraus ergeben sich die Kanten
Den resultierenden Graph zeigt Abbildung 13.2
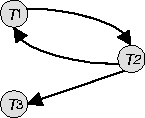
Abbildung
13.2: Der zu Historie H konstruierte Serialisierbarkeitsgraph
Da der konstruierte Graph einen Kreis besitzt, ist die Historie nicht
serialisierbar.



![]() mit insgesamt 14
Operationen.
mit insgesamt 14
Operationen.
