Betrachten wir das Index-File als Daten-File, so können wir dazu ebenfalls einen weiteren Index konstruieren und für dieses File wiederum einen Index usw. Diese Idee führt zum B*-Baum.
Ein B*-Baum mit Parameter ![]() wird charakterisiert durch folgende Eigenschaften:
wird charakterisiert durch folgende Eigenschaften:
Der Baum ![]() befindet sich im Hintergrundspeicher, und zwar
nimmt jeder Knoten einen Block ein. Ein Knoten mit
befindet sich im Hintergrundspeicher, und zwar
nimmt jeder Knoten einen Block ein. Ein Knoten mit ![]() Nachfolgern
speichert
Nachfolgern
speichert ![]() Paare von Schlüsseln und Adressen
Paare von Schlüsseln und Adressen
![]() . Es gilt
. Es gilt
![]() .
Eine Adresse in einem Blattknoten bezeichnet den Datenblock mit
den restlichen Informationen
zum zugehörigen Schlüssel, sonst bezeichnet sie den Block
zu einem Baumknoten: Enthalte der Block für Knoten
.
Eine Adresse in einem Blattknoten bezeichnet den Datenblock mit
den restlichen Informationen
zum zugehörigen Schlüssel, sonst bezeichnet sie den Block
zu einem Baumknoten: Enthalte der Block für Knoten ![]() die Einträge
die Einträge
![]() . Dann ist der erste Schlüssel im i-ten
Sohn von
. Dann ist der erste Schlüssel im i-ten
Sohn von ![]() gleich
gleich ![]() , alle weiteren Schlüssel
in diesem Sohn (sofern vorhanden) sind größer
als
, alle weiteren Schlüssel
in diesem Sohn (sofern vorhanden) sind größer
als ![]() und kleiner als
und kleiner als ![]() .
.
Wir betrachten nur die Operationen auf den Knoten des Baumes und nicht auf den
eigentlichen Datenblöcken. Gegeben sei der Schlüssel ![]() .
.
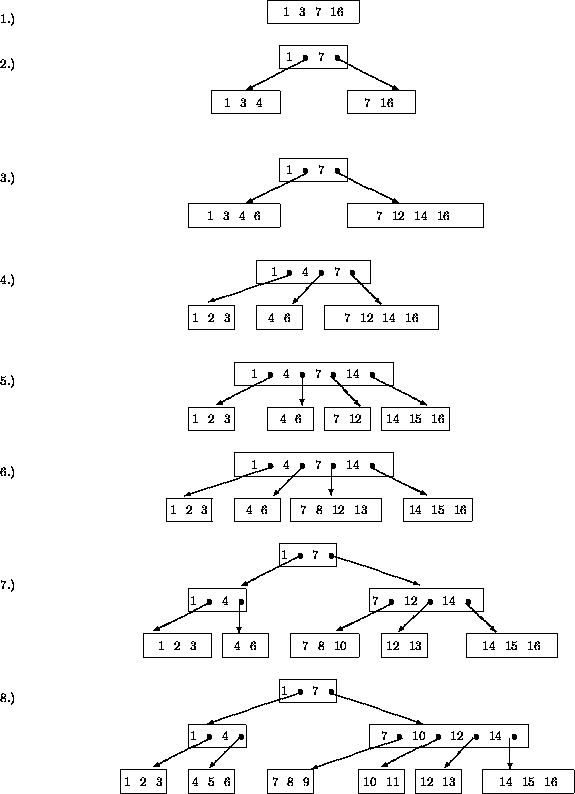
Abbildung 4.11 zeigt das dynamische Verhalten eines
B*-Baums mit dem Parameter ![]() .
Es werden 16 Schlüssel
eingefügt und 8 Schnappschüsse gezeichnet:
.
Es werden 16 Schlüssel
eingefügt und 8 Schnappschüsse gezeichnet:
Der Parameter ![]() ergibt sich aus
dem Platzbedarf für die Schlüssel/Adreßpaare
und der Blockgröße.
Die Höhe des Baumes ergibt sich aus der benötigten
Anzahl von Verzweigungen, um in den Blättern genügend
Zeiger auf die Datenblöcke zu haben.
ergibt sich aus
dem Platzbedarf für die Schlüssel/Adreßpaare
und der Blockgröße.
Die Höhe des Baumes ergibt sich aus der benötigten
Anzahl von Verzweigungen, um in den Blättern genügend
Zeiger auf die Datenblöcke zu haben.
Daraus errechnet sich der Parameter ![]() wie folgt
wie folgt
Die Wurzel sei im Mittel zu 50 % gefüllt (hat also
26 Söhne), ein innerer Knoten sei im Mittel zu
75 % gefüllt (hat also 39 Söhne), ein Datenblock
sei im Mittel zu 75 % gefüllt (enthält also 7
bis 8 Datenrecords).
300.000 Records sind also auf
![]() Datenblöcke verteilt.
Datenblöcke verteilt.
Die Zahl der Zeiger entwickelt sich daher auf den oberen Ebenen des Baums wie folgt:
| Ebene | Anzahl Knoten | Anzahl Zeiger | ||
| 0 | 1 | 26 | ||
| 1 | 26 | 26 |
= | 1.014 |
| 2 | 26 |
26 |
= | 39.546 |
Damit reichen drei Ebenen aus, um genügend Zeiger auf die Datenblöcke bereitzustellen. Der Platzbedarf beträgt daher
Das LOOKUP auf ein Datenrecord verursacht also vier Blockzugriffe: es werden drei Indexblöcke auf Ebene 0, 1 und 2 sowie ein Datenblock referiert. Zum Vergleich: Das Heapfile benötigt 30.000 Blöcke.
Soll für offenes Hashing eine mittlere
Zugriffszeit von 4 Blockzugriffen gelten,
so müssen in jedem Bucket etwa 5
Blöcke sein (1 Zugriff für Hash-Directory,
3 Zugriffe im Mittel für eine Liste von 5 Blöcken).
Von diesen 5 Blöcken sind 4 voll, der
letzte halbvoll. Da 10 Records in einen Datenblock passen,
befinden sich in einem Bucket etwa
![]() Records.
Also sind
Records.
Also sind
![]() Buckets erforderlich.
Da 256 Adressen in einen Block passen, werden
Buckets erforderlich.
Da 256 Adressen in einen Block passen, werden
![]() Directory-Blöcke benötigt.
Der Platzbedarf beträgt daher
Directory-Blöcke benötigt.
Der Platzbedarf beträgt daher
![]() .
.
Zur Bewertung von B*-Bäumen läßt sich sagen: