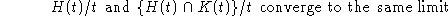
Perhaps the most important result about the contact process is the
Complete Convergence Theorem. When the contact process does not die out then it will converge to the stationary distribution that is the limit starting from all 1's.
An immediate conseqeunce of this is that the only stationary distributions for the process are (i) the limit starting from all 1's, (ii) the trivial stationary distribution which assigns probability one to the all 0's configuration and (iii) p times (i) plus (1-p) times (ii).
As in the case of Richardson's model and the biased voter model, there is a.
Shape Theorem. If we start from B(0) = a finite set, B, and B(t) does not not die out, then B(t)/t has a limiting shape. Furthermore inside the linearly growing ball, B(t), the system is close to the nontrivial stationary distribution.
To formulate this result precisely, we define two contact processes: one we call state^1_t[x] starting from all 1's, and one we call state^B_t[x] starting from the finite set B on the same space by using the same birth and death events to drive both processes. The attractive property of the contact process implies that that state^1_t[x] is always larger than state^B_t[x].
If we let H(t) (for "hit by time t") be the set of sites that have been 1 at some time s < t in state^B_t[x] then state^B_t[x] = 0 outside H_t so it is far from equilibrium there. Let K(t) (for "coupled at time t") be the set of sites where state^1_t[x] = state^B_t[x]. The precise statement of the shape theorem for the contact process is that:
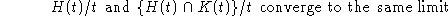
We have to take the intersection with H(t) since K(t) contains all the points outside of H(t) where state^1_t[x]=0. In words this result says that the two processes agree over most of H(t), which is the largest region on which we can sensibly expect to have agreement with the process starting from all 1's.
s3 Exercise. To see the shape theorem, pick "CP Shape Theorem" from the model menu. Sites that have not been hit by the process state^B are black if state^1_t[x] = 0 and dark green if state^1_t[x] = 1. Sites where the two processes agree are gray if both are 0 and light green if both are 1. The bad sites, i.e., those that have been hit but have state^B_t[x] = 0 while state^1_t[x] = 1 are light blue. However there are only a few of these near the boundary.
History Lesson. These reults were first proved in one dimension by Durrett (1980). Durrett and Griffeath (1982) proved them for values of delta below the critical value delta_c(Z) for the one dimensional contact process on the integer lattice. Durrett and Schonman (1987) exteneded the result to delta's below the critical value delta_c(Z x {1, ... L}) for the contact process on a strip of width L. Finally, Bezuidenhout and Grimmett (1990) completed the proof by showing that as L tends to infinity the strip critical values converge to the critical value for the plane. Durrett (1992) gives an account of these developments.
Durrett, R. (1980) On the growth of one dimensional contact processes. Ann. Prob. 8, 890-907
Durrett, R. and Griffeath, D. (1982) Contact processes in several dimensions. Z. fur Wahr. 59 535-552
Durrett, R. and Schonmann, R.H. (1987) Stochastic growth models. In Percolation Theory and the Ergodic Theory of Interacting Particle Systems. Edited by H. Kesten. Springer Verlag, New York
Bezuidenhout, C. and Grimmett, G. (1990) The critical contact process dies out. Ann. Prob. 19, 984-1009
Durrett, R. (1992) The contact process: 1974--1989. Pages 1-18 in Mathematics of Random Media. Edited by W.E. Kohler and B.S. White, American Math. Society