Definere:
Für
0![]() f
f![]() 1 sei der f -Punkt der Kante (r,s) der Punkt, der
f · c(r,s) Einheiten
von r bzw.
(1 - f ) · c(r,s) Einheiten von s entfernt ist.
1 sei der f -Punkt der Kante (r,s) der Punkt, der
f · c(r,s) Einheiten
von r bzw.
(1 - f ) · c(r,s) Einheiten von s entfernt ist.
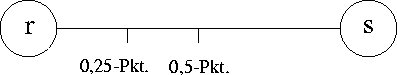
Betrachte nun die kürzeste Entfernung von einem Knoten j zu allen
f -Punkten der Kante (r,s) . Es ergibt sich eine Funktion
(d'(j,(r,s)))(f ) , wobei f ![]() [0,1] ist. Wir unterscheiden nun in zwei Fälle:
[0,1] ist. Wir unterscheiden nun in zwei Fälle:
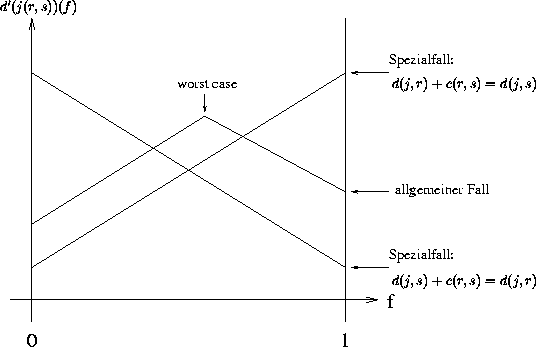
Die Frage ist nun, wie man den worst case, also die maximale Entfernung von
j zu einem Kantenpunkt f , berechnet. Es leuchtet ein, daß diese maximale
Entfernung
max [j,(r,s)] gegeben ist durch
max[j,(r,s)] = ![]() [d (j,r) + c(r,s) + d (j,s)] .
[d (j,r) + c(r,s) + d (j,s)] .
Nun ist es leicht, das generelle Zentrum von G = (V,E) zu bestimmen, es ist
der Knoten i mit minimalem
max {max[i,(x,y)]|(x,y) ![]() E} .
E} .