Der Beweis dieser Behauptung folgt aus der folgenden Skizze:
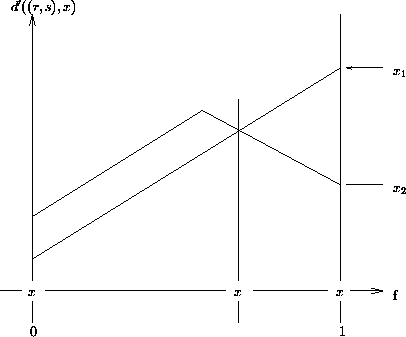
Diese Skizze entspricht der Darstellung der Funktionen, die bei der Berechnung des absoluten Zentrums eine Rolle spielen. Es ist einleuchtend, daß ein potentieller m -Zentrums-Punkt nur einer der mit einem Kreuz markierten Punkte sein kann. Für diese Punkte gilt aber genau die oben gemachte Behauptung.
Es ergibt sich also nur eine endliche Menge von Zentrumskandidaten
K = {p1,...,pk} . Bilde jetzt die Matrix
wij : = d (pj,vi) für alle
vi ![]() V,pj
V,pj ![]() K und wähle m Kandidaten
{p1,...,pm} : = M als
erstes vorläufiges m-Zentrum. Sei
gM : = max {min {wij|pj
K und wähle m Kandidaten
{p1,...,pm} : = M als
erstes vorläufiges m-Zentrum. Sei
gM : = max {min {wij|pj ![]() M}|i
M}|i ![]() V} .
V} .
Die entscheidende Frage ist nun, ob dieses gM noch zu unterbieten ist.
Um dieser Frage nachzugehen, bilden wir nun eine boolesche Matrix aij ,
deren Element gleich 1 ist, wenn wij < gM gilt, und gleich 0 ist im
anderen Fall. In dieser Matrix suchen wir nun eine Spaltenüberdeckung, d.h.
eine Menge M1 von Spalten mit
![]() aij > 0
aij > 0![]() i
und minimaler Kardinalität von M1 .
i
und minimaler Kardinalität von M1 .
Falls die errechnete Spaltenüberdeckung mehr als m Spalten hat, so war M
bereits optimal, d.h., gM war schon der minimale Wert für ![]() .
.
Finden wir jedoch eine Spaltenüberdeckung mit m oder weniger Spalten, so haben wir ein neues, besseres m -Zentrum gefunden. Dieses neue m -Zentrum unterziehen wir nun erneut dieser Prozedur, bis wir kein neues m -Zentrum mehr finden. Dieser Abbruch erfolgt auf jeden Fall nach endlich vielen Iterationen, da in jeder Iteration die Anzahl der Einsen in (a)ij abnimmt.