Der zur ![]() -Achse symmetrische Zylinder mit Höhe 2 und Radius 1 besteht aus
einer Mantelfläche und zwei Deckflächen.
Die beiden Kreisscheiben bei
-Achse symmetrische Zylinder mit Höhe 2 und Radius 1 besteht aus
einer Mantelfläche und zwei Deckflächen.
Die beiden Kreisscheiben bei
![]() und
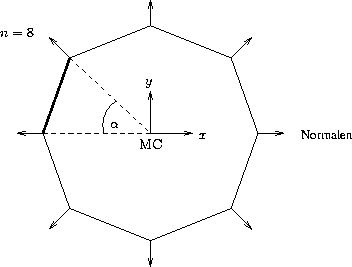
und ![]() lassen sich durch regelmäßige
lassen sich durch regelmäßige ![]() -Ecke
darstellen.
Die Mantelfläche wird durch
-Ecke
darstellen.
Die Mantelfläche wird durch ![]() Rechtecke approximiert.
Dabei wachsen mit
Rechtecke approximiert.
Dabei wachsen mit ![]() sowohl die Genauigkeit der Approximation
als auch der Rechenaufwand.
Sei
sowohl die Genauigkeit der Approximation
als auch der Rechenaufwand.
Sei
![]() , so lauten für ein solches Rechteck die vier Eckpunkte
und die zugehörigen Normalenvektoren:
, so lauten für ein solches Rechteck die vier Eckpunkte
und die zugehörigen Normalenvektoren:
| Eckpunkt | Normalenvektor |
|
|
|
|
|
|
|
|
|
|
|
|
mit
![]() ,
,
![]() .
.
Als Normalenvektor in einem Eckpunkt dieser
Fläche wird also der tatsächliche
Normalenvektor der Mantelfläche genommen.
Dadurch erhalten
aneinandergrenzende Flächen in ihren gemeinsamen Eckpunkten auch
denselben Normalenvektor.
Auf diese Weise erzeugt das Programm bei der späteren Beleuchtung
den Eindruck eines
stetigen Übergangs zwischen den Flächen.
Der Betrachter nimmt statt
einer ![]() -eckigen Säule den Zylinder wahr.
-eckigen Säule den Zylinder wahr.