Die in Kapitel 7.3 eingeführten Bezier-Kurven können auch zur
Definition einer gekrümmten Fläche im Raum verwendet werden.
Da eine Fläche zweidimensional ist, muß eine weitere Parameterdimension
hinzugefügt werden, d.h. statt
![]() gilt nun
gilt nun
![]() .
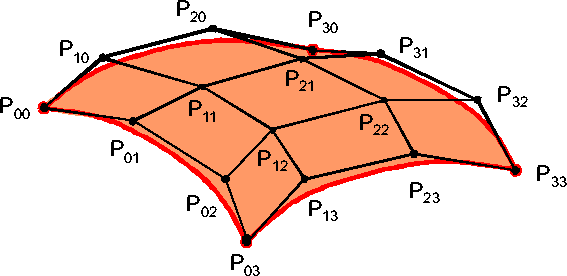
Im folgenden Beispiel werden 16 Kontrollpunkte mit kubischen Bernsteinpolynomen
gewichtet:
.
Im folgenden Beispiel werden 16 Kontrollpunkte mit kubischen Bernsteinpolynomen
gewichtet:
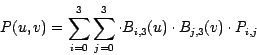
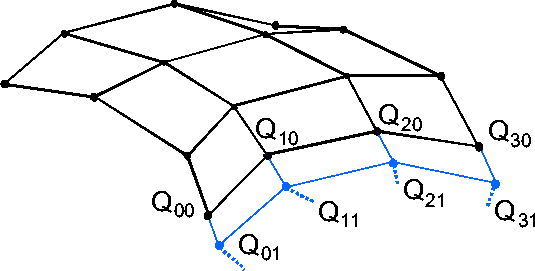
Beim Verlängern einer Bezier-Fläche ist darauf zu achten,
dass die neue Reihe von Kontrollpunkten tangential die bisherige
Fläche verlängert, d.h.
![]() sind collinear und das Verhältnis der Abstände
sind collinear und das Verhältnis der Abstände
![]() ist konstant.
ist konstant.