Da ![]() und
und ![]() zwei Punkte auf einer Geraden sind, bietet es sich an,
die ganze Linie als Teilstück einer Geraden aufzufassen und durch die
Parametrisierung der Geraden mit einem Parameter
zwei Punkte auf einer Geraden sind, bietet es sich an,
die ganze Linie als Teilstück einer Geraden aufzufassen und durch die
Parametrisierung der Geraden mit einem Parameter ![]() die Pixel zu bestimmen.
die Pixel zu bestimmen.
Gesucht ist der Vektor ![]() , der von
, der von ![]() nach
nach ![]() führt.
führt.
Es gilt
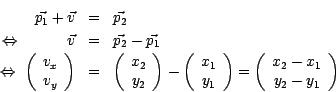
Die gesamte Gerade ![]() ergibt sich, wenn man von
ergibt sich, wenn man von ![]() zu einem Punkt der
Geraden geht (z.B.
zu einem Punkt der
Geraden geht (z.B. ![]() ) und von dort ein beliebiges Vielfaches des
Richtungsvektors
) und von dort ein beliebiges Vielfaches des
Richtungsvektors ![]() abträgt (Punkt-Richtungsform):
abträgt (Punkt-Richtungsform):
Die gesuchte Linie ![]() erhält man, wenn man
erhält man, wenn man ![]() auf das
Intervall
auf das
Intervall
![]() beschränkt:
beschränkt:
Jetzt muß man nur noch entscheiden, in wievielen Schritten ![]() das
Intervall
das
Intervall
![]() durchlaufen soll; d.h. wieviele Pixel man
''anschalten'' will, um die ganze Linie zu repräsentieren.
durchlaufen soll; d.h. wieviele Pixel man
''anschalten'' will, um die ganze Linie zu repräsentieren.
Eine von ![]() und
und ![]() unabhänigige Anzahl (z.B. 100 Schritte) würde bei
kurzen Linien dazu
führen, daß manche Pixel aufgrund der Rundung mehrfach gesetzt würden. Bei langen Linien
hingegen wären die Pixel evtl. nicht benachbart.
unabhänigige Anzahl (z.B. 100 Schritte) würde bei
kurzen Linien dazu
führen, daß manche Pixel aufgrund der Rundung mehrfach gesetzt würden. Bei langen Linien
hingegen wären die Pixel evtl. nicht benachbart.
Sinnvoll wäre es, soviele Pixel zu setzen, wie die Linie Einheiten lang
ist. In der euklidischen Ebene ist die Länge ![]() einer Strecke
einer Strecke
![]() als Abstand von
Anfangs- und Endpunkt definiert.
Die Abstandsberechnung geschieht mit Hilfe der euklidischen Norm
(vgl. Pythagoras):
als Abstand von
Anfangs- und Endpunkt definiert.
Die Abstandsberechnung geschieht mit Hilfe der euklidischen Norm
(vgl. Pythagoras):
Hier die draw-Methode der Klasse line.VectorLine. ![]() ,
,
![]() ,
, ![]() und
und ![]() sind int-Variablen, die bei der Instanziierung
der Linie übergeben wurden. D.h. die Linie weiß, wo sie beginnt und wo
sie aufhört und kann sich selber zeichnen.
sind int-Variablen, die bei der Instanziierung
der Linie übergeben wurden. D.h. die Linie weiß, wo sie beginnt und wo
sie aufhört und kann sich selber zeichnen.
public void draw(CGCanvas cgc) {
int x, y, dx, dy;
double r, step;
dy = y2 - y1; // Hoehenzuwachs
dx = x2 - x1; // Schrittweite
step = 1.0 / Math.sqrt(dx*dx + dy*dy); // Parameterschritt berechnen
for(r=0.0; r < 1; r+=step) { // fuer jeden Parameterwert
x = (int)(x1 + r*dx +0.5); // berechne neue x-Koordinate
y = (int)(y1 + r*dy +0.5); // berechne neue y-Koordinate
cgc.setPixel(x,y); // setze Pixel
}
cgc.setPixel(x2, y2); // letztes Pixel am Endpunkt
}
|
Diese Implementation hat den Nachteil, daß sehr viel Gleitkommaarithmetik durchgeführt werden muß. Gleitkommaarithmetik ist (in Java) im Gegensatz zu Integerarithmetik sehr zeitintensiv. Wir werden im Folgenden diesen Nachteil schrittweise beseitigen.