Eigentlich ist es unnötig für jedes Pixel die neue ![]() -Koordinate und
die neue
-Koordinate und
die neue ![]() -Koordinate auszurechnen, da man ja der Reihe nach alle Pixel der
Linie setzen will. Wenn man also für jedes Pixel z.B. die
-Koordinate auszurechnen, da man ja der Reihe nach alle Pixel der
Linie setzen will. Wenn man also für jedes Pixel z.B. die ![]() -Koordinate
um
-Koordinate
um ![]() erhöht, braucht man nur noch die zugehörige
erhöht, braucht man nur noch die zugehörige ![]() -Koordinate zu
berechnen. Dazu muß die Geradengleichung aber in Form einer Funktion
vorliegen:
-Koordinate zu
berechnen. Dazu muß die Geradengleichung aber in Form einer Funktion
vorliegen:
Die Steigung ![]() errechnet sich mit dem Steigungsdreieck wie folgt:
errechnet sich mit dem Steigungsdreieck wie folgt:
das gilt sowohl für das Dreieck mit ![]() und
und ![]() als auch für das
Dreieck mit
als auch für das
Dreieck mit ![]() und dem Punkt
und dem Punkt ![]() , an dem die Gerade die
, an dem die Gerade die ![]() -Achse
schneidet:
-Achse
schneidet:
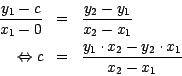
einsetzen in die Geradengleichung ergibt:
Hier die draw-Methode aus der Klasse line.StraightLine:
public void draw(CGCanvas cgc) {
int x, y;
double s, c;
s = (double)(y2 - y1) / (double)(x2 - x1); // Steigung berechnen
c = (double)(y1*x2 - y2*x1) / // y-Achsenabschnitt
(double)(x2 - x1);
x = x1; // Koordinaten retten
y = y1;
if(x < x2) { // Linie links -> rechts
while(x <= x2) { // fuer jede x-Koordinate
y = (int)(s*x + c + 0.5); // berechne y-Koordinate
cgc.setPixel(x,y); // setze Pixel
x++; // naechste x-Koordinate
}
}
else { // Linie rechts -> links
while(x >= x2) { // fuer jede x-Koordinate
y = (int)(s*x + c + 0.5); // berechne y-Koordinate
cgc.setPixel(x,y); // setze Pixel
x--; // naechste x-Koordinate
}
}
}
|
Diese Version kommt mit ungefähr halb soviel Gleitkommaarithmetik aus, wie die letzte. Allerdings brauchen wir eine zusätzliche Fallunterscheidung, um zu klären, ob die Linie von links nach rechts verläuft oder andersherum. Ein weiterer schwerer Nachteil liegt in der Tatsache, daß die Pixel für steile Geraden nicht benachbart sind.