



Für jede Fläche 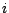 liege nun ihre
Radiosity
liege nun ihre
Radiosity
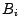 vor.
Hieraus interpoliert man die
Strahlung
für die Eckpunkte:
vor.
Hieraus interpoliert man die
Strahlung
für die Eckpunkte:
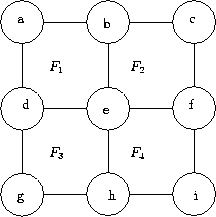
Nun wird jedes Patch in zwei Dreiecke zerteilt, so daß nach der Projektion
die Strahlungswerte an den Dreiecksecken zur zweifachen Interpolation verwendet
werden können.



