prev up inhalt next

Erzeugung einer bildbezogenen Farbtabelle

Gegeben sei ein Bild mit einer Menge $F$ von beobachteten Farben. Es sei $n = \vert F\vert$die Anzahl der verschiedenen Farben in dem Bild. Wenn der Videocontroller zwar alle $n$ Farben darstellen kann, aus Platzgründen aber dennoch eine Farbtabelle benötigt wird, so ist es sinnvoll die Farben so zu wählen, daß sie das gegebene Bild möglichst gut repräsentieren.

Zunächst wird für jede Farbe die Häufigkeit ihres Auftretens ermittelt. Ggf. muß ``vorquantisiert'' werden von 24 Bit auf 15 Bit (je 5 Bit für Rot, Grün, Blau); hierdurch erhält das Histogramm maximal 32768 Einträge. Sei $d(a, b)$ der Abstand zweier Farbtupel $a, b$, z.B.

\begin{displaymath} \sqrt{(a_{Rot} - b_{Rot})^{2} + (a_{Gruen} - b_{Gruen})^2 + (a_{Blau} - b_{Blau})^2}. \end{displaymath}



Optimaler Algorithmus

Gegeben sei eine Menge $F$ von beobachteten Farben. Gesucht ist eine Menge $M$ von Repräsentanten, so daß der Ausdruck

\begin{displaymath} \Delta := \max \limits_{x \in F}\ \ \min \limits_{p \in M} d(p, x) \end{displaymath}

minimiert wird, d.h., $\Delta$ ist der maximale Abstand, den eine Farbe zu ihrem nächsten Repräsentanten hat.

Da die exakte Bestimmung von $M$ eine exponentielle Laufzeit verursacht, begnügt man sich mit einer Näherungslösung.



Popularity-Algorithmus (1978)

Wähle die $K$ häufigsten Farben.

Nachteil: Selten vorkommende Farben werden schlecht repräsentiert.



Diversity-Algorithmus ($xv$, John Bradley, 1989) 


Initialisiere M mit der häufigsten Farbe


for i := 2 to K do


erweitere M um die Farbe des Histogramms,


die zu allen Farben aus M den größten Abstand hat


end



Median-Cut (Heckbert, MIT 1980)

Ziel:
Finde $K$ Repräsentanten, die jeweils möglichst gut gleich viele Farben repräsentieren.

Idee:
Zerlege den RGB-Würfel mit den beobachteten Farbhäufigkeiten solange sukzessive in Unterwürfel durch Aufsplitten an einer Trennfläche, bis $K$ Unterwürfel entstanden sind. 





Initialisiere RGB-Wuerfel mit Häufigkeiten der beobachteten Farbtupel


Initialisiere Wurzel des Schnittbaums mit Gesamtzahl der Pixel


While noch_nicht_genügend_Blätter do


Wähle Blatt mit der größten Pixelzahl


Bestimme umschliessende Box


Bestimme Achse mit größtem Wertebereich


Durchlaufe Box längs dieser Achse


Teile am Median in zwei Hälften


Trage Hälften als Soehne ein


end


Für jedes Blatt wähle den Mittelwert aller in ihm liegenden Farben.

Wenn das Bild $n$ verschiedene Farben enthält und diese durch $K$ verschiedene Farben repräsentiert werden sollen, dann liegt die Laufzeit in $O(n \log K)$.


Abbildung 9.3: Partitionierung der Ebene beim Median-Cut-Algorithmus

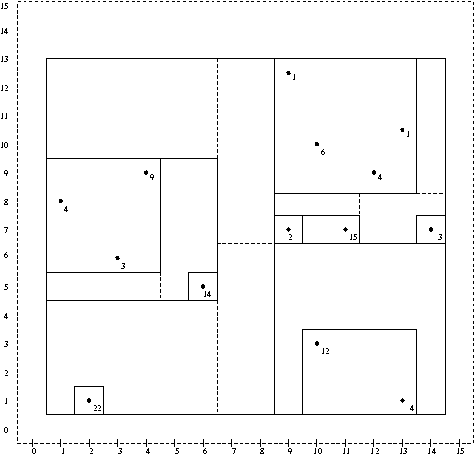
Abbildung 9.3 zeigt die Anwendung des Median-Cut-Algorithmus anhand eines Beispiels. Zur einfachen Darstellung ist der Farbbaum zweidimensional gewählt. Gezeigt wird die Verteilung der Farbtupel aus dem Bereich $[0 \ldots 15] \times [0 \ldots 15]$ in einem Bild mit $10 \times 10 = 100$ Pixeln. Eingetragen sind an der Position $x/y$ die Häufigkeit des Farbtupels $x, y$. Schnittlinien sind gestrichelt, umschließende Boxen durchgezogen gezeichnet.


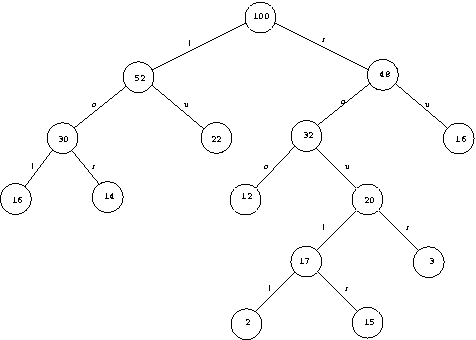
Abbildung 9.4: Schnittbaum beim Median-Cut-Algorithmus

Abbildung 9.4 zeigt für das vorliegende Beispiel den Schnittbaum nach Anwendung des Median-Cut-Algorithmus. Die Knoten sind markiert mit der Anzahl der noch zu quantisierenden Pixel, an den Kanten ist vermerkt, ob es sich um einen Links/Rechts- oder um einen Oben/Unten-Schnitt handelt.

Floyd-Steinberg-Dithering (1975)
Der bei Verwendung einer Farbtabelle verursachte Fehler beim Quantisieren eines Pixels wird auf die Nachbarpixel verteilt (bevor diese quantisiert werden). 

for (i = 0; i < M; i++)
for (j = 0; j < N; j++)
{
   x = f[i][j];   /* hole Original-Farbe */
   k = p(x);      /* finde naechsten Repraesentant */
   q[i][j] = k;   /* zeichne quantisiertes Pixel */
   e = d(x, k);   /* bestimme Fehlerabstand */
   f [i][j + 1]     = f[i][j + 1]     + e * 3.0/8.0;
   f [i + 1][j]     = f[i + 1][j]     + e * 3.0/8.0;
   f [i + 1][j + 1] = f[i + 1][j + 1] + e * 1.0/4.0;
}



24 Bit pro Pixel,
16 Mill. Farben

8 Bit pro Pixel,
256 Farben



4 Bit pro Pixel,
16 Farben

2 Bit pro Pixel,
4 Farben
Auswirkung des Median-Cut-Algorithmus

Abbildung 9.3 zeigt Original und quantisierte Versionen einer $14 \times 14$ Ausschnittvergrößerung, erstellt von einem $814 \times 517$ True-Color-Bild. Die Zahl der Farben bezieht sich jeweils auf das Gesamtbild. Verwendet wurde der Median-Cut-Algorithmus mit anschließendem Floyd-Steinberg-Dithering.

prev up inhalt next