Tesselation

Vortrag im Rahmen des Seminars Computergrafik II

Leiter: Dipl.-Phys. Olaf Müller

Student: Amir Sekic

Tesselation

Tesselation ist eine Technik, die sich mit der Zerlegung von Polygonen beschäftigt. Dabei spielen die Genauigkeit, die Schnelligkeit und die Einfachheit eine große Rolle, wie auch bei den meisten anderen, Polygone bearbeitenden, Techniken wie Consolidation und Simplification.

Die Polygone werden bei der Tesselierung in so genannte primitive Flächen, wie z.B. Dreiecke oder Vierecke zerlegt, da solche Flächen leichter zu handhaben sind als komplexe Polygone (insbesondere konkave).

Die Dreieckszerlegung der Polygone nennt man auch Triangulation.

Das englische Wort to tesselate kommt ursprünglich aus dem lateinischen und bedeutet mit Mosaik pflastern, mit einem Muster überziehen.

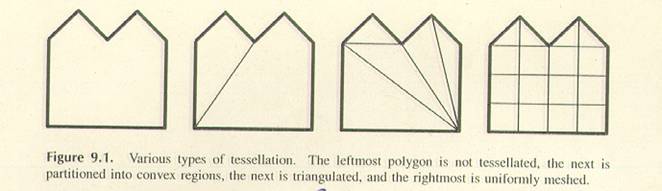
Es gibt verschiedene Typen von Tesselation, die man in folgendem Bild sehen kann.

Wieso tesseliert man?

Die meisten heutigen Grafik-APIs und Grafikkarten sind optimiert für Dreiecke. Da Dreiecke planar und konvex sind wird das Scanline-Verfahren nur auf Dreiecke angewandt, was zur Vereinfachung und Beschleunigung des Renderings führt. Wenn man auf die komplexeren Polygone das Scanline-Verfahren anwenden will, ist der Aufwand etwas großer, wobei die Hohlräume und Kantenüberschneidungen zusätzlich eine Rolle spielen.

Manche APIs arbeiten auch auf konvexen Polygonen, was keine große Rolle spielt, da der Aufwand um ein konvexes Polygon in Dreiecke zu zerlegen sehr klein ist. Ein konvexes Polygon lässt sich triangulisieren, indem man von einem beliebigen Eckpunkt aus zu allen nicht benachbarten Eckpunkten Diagonalen zieht.

Wenn man bei einer Fläche Schatten und Beleuchtung besser regulieren will, kann man ein Netz über die Fläche ziehen, was zur einer besseren Bildqualität führt.

Tesselation ist nur dann sinnvoll, wenn man kleine Teile der Fläche separieren will, um diese getrennt zu bearbeiten.

Um eine Tesselierung durchzuführen, entwickelt man sogenannte Tesselators, worauf im ersten Kapitel weiter eingegangen wird.

In den anderen Kapiteln wird auf einzelne Probleme näher eingegangen; sowohl auf solche, die gelegentlich beim korrekten Tesselieren auftreten, wie auch derartige, die beim falschen Tesselieren entstehen können.

1.0 Tesselators

Unter dem Oberbegriff Tesselators verbergen sich alle voneinander verschiedenen Implementierungen zur Tesselation. Einen robusten und vor allem generellen Tesselator zu implementieren ist sehr schwierig. Beim Tesselieren können zwei Probleme auftreten, welche man manchmal nicht so leicht vermeiden kann.

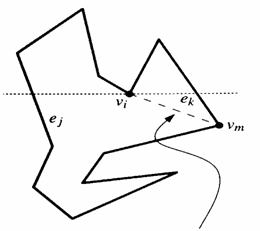
Das erste Problem entsteht beim Projezieren, wenn sich zwei Kanten bei einem Viereck überschneiden.

Das zweite entsteht wenn ein Polygon mehrere äußere und nur eine innere Region hat, wenn also ein Polygon Hohlräume besitzt.

Nach dem Testen auf diese zwei Probleme kommt man zur eigentlichen Aufgabe, der Dreieckszerlegung. Eine Methode wird im Kapitel Polygon Triangulation vorgestellt.

1.1 Kantenüberschneidungen ( self-intersection )

Das Erste, was ein Tesselator tun soll, ist herauszufinden, wie man ein 3-D Polygon am besten in 2-D projezieren kann.

Damit werden das Problem der Zerlegung in simple Polygone und der zugehörige Algorithmus vereinfacht.

Eine Methode ist eine der x, y, z Koordinaten zu löschen, das heißt das Polygon wird in eine der xy, xz, oder yz Ebenen projeziert.

Meistens ist die Projektionsseite mit der größten Projektionsfläche die beste (man benutzt die gleiche Technik wie für den Punkt im Polygon Test). Dabei ist die Gefahr einer self-intersection viel kleiner.

Die Fläche kann direkt berechnet werden oder man setzt die Koordinate der Normale mit dem größten Betrag auf Null.

Betrachtet man zum Beispiel eine Normale mit den Koordinaten (-6, 2, 4), so nimmt man die x-Koordinate (–6), den sie hat den größten Betrag.

Dieses Verfahren eliminieren die meisten, aber nicht alle Kantenüberschneidungen.

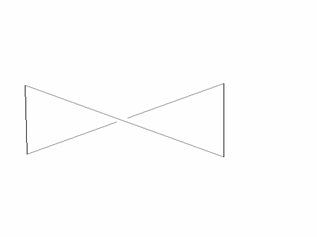
Bei Kantenüberschneidungen entsteht ein sogenanntes Bowtie –Viereck (siehe Bild unten).

Von der theoretischen Seite her kann man folgendermaßen überprüfen, ob Kantenüberschneidungen vorliegen:

Seien f₁(s) = r₁ + s*d₁ und f₂(t) = r₂ + t*d₂ zwei parametrisierte Gradengleichungen .

Wenn man setzt :

1: f₁(s) = f₂(t)

2: r₁ + s∙d₁ = r₂ + t∙d₂

Multipliziert man einmal mit dem Vektor d₂ ^{^} , der orthogonal zu d₂ ist, und einmal mit dem Vektor d₁ ^{^} , der orthogonal zu d₁ ist, erhält man folgendes:

3: s∙d₁ * d₂ ^{^} = ( r₁ - r₂ ) * d₂ ^{^} da d₁ * d₁ ^{^} = 0 und d₂ * d₂ ^{^} = 0

t∙d₂ * d₁ ^{^} = ( r₁ - r₂ ) * d₁ ^{^}

“ * ” - bezeichnet den Skalarprodukt

4: s = ( r₂ - r₁ ) * d₂ ^{^} / ( d₁ * d₂ ^{^} )

t = ( r₁ - r₂ ) * d₁ ^{^} / ( d₂ * d₁ ^{^} )

Wenn d₁ * d₂ ^{^} = 0 (dann ist d₂ * d₁ ^{^} auch Null) also d₁ und d₂ parallel sind, dann sind die Geraden auch parallel. Das heißt, wenn s und t endlich groß sind, schneiden sich die Geraden.

Für endlich lange Strecken der Länge l₁ und l₂ die in p₁ und q₁ (s = t = 0) starten und in p₂ und q₂

(s = l₁ , t = l₂ ) enden, erhält man folgendes:

r₁ =p₁, d₁ = p₂ – p₁, r₂ =q₁, d₂ = q₂ – q₁ t = (r₁ - r₂ ) * d₁ ^{^} / (d₂ * d₁ ^{^} ) .

Wenn t und s aus [0,1] sind, dann schneiden sich die beiden Linien f₁(s) und f₂(t), sonst nicht.

Von der praktischen Seite aus gesehen, stellt sich diese Tatsache dann folgendermaßen dar:

Wir verwenden die gleiche Notation wie oben:

Seien f₁(s) = p₁ + s∙( p₂ - p₁ ) und f₂(t) = q₁ + t∙( q₂ - q₁ ) die zwei Linien (Polygonkanten)

Wenn man das gleiche Verfahren wie oben für f₁(s) = f₂(t) benutzt, erhält man Folgendes:

s = ( - c * a^{^} ) / ( b * a^{^} ) = ( c * a^{^} ) / ( a * b^{^} ) = d / f

t = ( c * b^{^} ) / ( a * b^{^} ) = e / f

Wobei a = q₂ – q₁, b = p₂ – p₁, c = p₁ – q₁, d = c * a^{^}, e = c * b^{^} und f = a * b^{^} ,

a^{^} und b^{^} sind Vektoren die orthogonal zu a und b sind.

Das Vereinfachen des Faktors s geschieht mit Hilfe von a^{^} * b = - b^{^} * a und a * b^{^} = b^{^} * a .

Wenn a * b^{^} = 0, sind die Linien kollinear.

Solange man s und t nicht explizit braucht, kann man folgenden Code benutzen, um zu testen,

ob 0 £ s £ 1 :

if ( f > 0 )

If (d < 0 or d > f ) return NO_INTERSECTION;

else

if (d > 0 or d < f ) return NO_INTERSECTION;

Bei diesem Test wird die Division vermieden, was zur Verbesserung der Effizienz führt.

Nach diesem Test ist sichergestellt, dass 0 £ s £ 1 .

Entsprechendes prüft man für t = e / f (d tauscht man durch e aus). Wenn der Test kein NO_INTERSECION liefert, bedeutet das, dass sich die Linien schneiden.

In dem Fall versucht man das Polygon in eine andere Projektionsebene zu projezieren.

1.3 Hohlräume

Die Idee, Hohlräume zu beseitigen ist folgende: Man verbindet zwei Vertizes, welche sich auf verschiedenen Kanten befinden, wobei die Kanten verschiedene äußere Regionen haben.

Dabei soll ein einfaches Polygon entstehen. Man erhält dann ein Polygon mit nur noch einer inneren und einer äußeren Region.

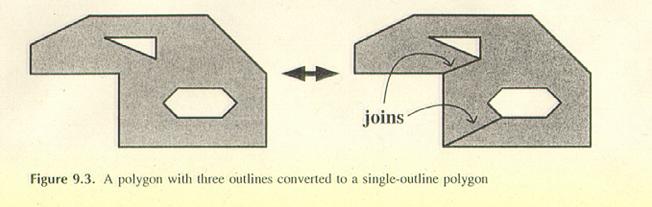
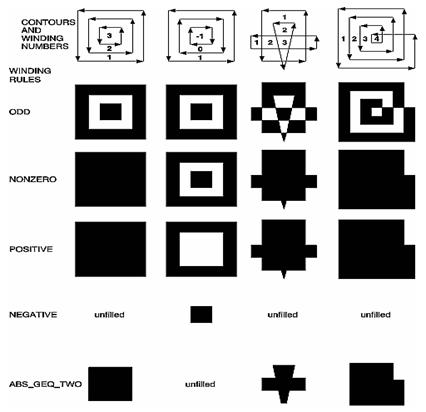
Bei Hohlräumen ist außerdem die (winding number) Umlaufzahl zu beachten.

Die Umlaufzahl gibt an, wie oft der Punkt von der Kontur des Polygons umlaufen wird, bzw. wie viele Konturen ihn umschließen.

Ein Umlauf gegen den Uhrzeigersinn wird (für einen Bereich und alle weiteren inneren Bereiche) positiv angerechnet, ein Umlauf im Uhrzeigersinn negativ.

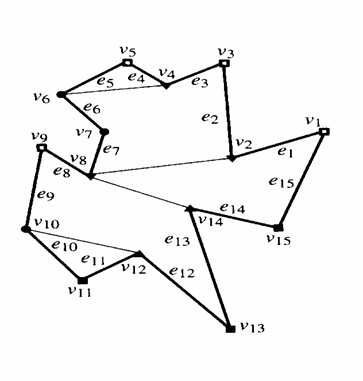
Hierbei geht man von Außen nach Innen vor. Für jeden Punkt in einem Bereich ist die Umlaufzahl natürlich gleich. Das Bild zeigt Beispiele für Polygone mit Regionen und deren Umlaufzahl.

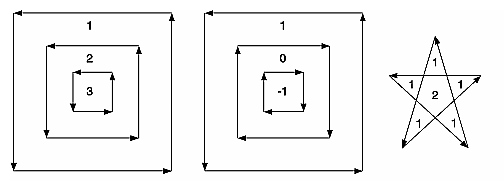
Die Umlaufregel klassifiziert einen Bereich als Innen, wenn die Umlaufzahl zu einer bestimmten gewählten Kategorie gehört. Unterschieden werden dabei folgende Kategorien: ungerade, ungleich null , positiv, negativ und Betrag ³ 2.

Durch diese Kategorien werden Teile des Polygons als Außen und andere Teile als Innen definiert. Die Wahl der Kategorie bestimmt also wo Außen und wo Innen ist.

Meistens werden die Kategorien „ungerade“ oder „ungleich null“ verwendet, um das Innere eines Polygons zu bestimmen.

Das Bild zeigt für alle Kategorien einige Beispiele, wie die Polygone bei dieser Wahl aufgeteilt werden.

1.4 Polygon Triangulation

In diesem Teil wird die Dreieckszerlegung von Polygonen ohne Kantenüberschneidungen und Hohlräume behandelt. Man geht hierbei davon aus, dass alle Kantenüberschneidungen und Hohlräume durch die oben beschriebenen Verfahren beseitigt worden sind.

Der erste Schritt in diesem Verfahren ist die Zerlegung in sogenannte monotone Regionen (Polygone). Im zweiten Schritt werden dann die monotonen Teile in Dreiecke zerlegt.

Definition: Ein Polygon ist monoton in Beziehung zur Linie l wenn für jede Linie l^| , die orthogonal zur Linie l ist, beim Schneiden mit dem Polygon eine Linie oder ein Punkt entsteht.

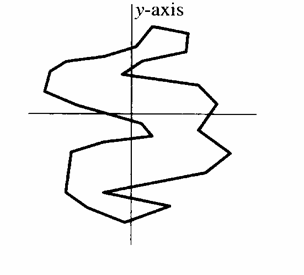
Definition: Punkt p ist oberhalb von q, wenn p_y £ q_y und p_x > q_x ,und p ist unterhalb von q, wenn p_y ³ q_y und p_x < q_x .

Hierbei sind p_x und q_x die jeweiligen x-Werte von p und q, p_y und q_x die jeweiligen y-Werte.

Wir können ein Polygon folgendermaßen in monotone Regionen zerlegen:

Man beginnt beim Vertex mit dem größten y-Wert und folgt dann der Polygonkante im Uhrzeigersinn. Ein Vertex, bei dem wir die Richtung von oben nach unten oder von unten nach oben ändern, bezeichnen wir als Turn Vertex.

Es werden fünf verschiedene Arten von Turn Vertizes definiert:

Einen Start-Vertex hat man, wenn die Nachbarn unterhalb liegen und der innere Winkel ß < 180° ist .

Einen End-Vertex, wenn die Nachbarn oberhalb liegen und ß < 180°.

Einen Split-Vertex, wenn die Nachbarn unterhalb liegen und ß > 180°.

Einen Merge-Vertex, wenn die Nachbarn oberhalb liegen und ß > 180°.

Alle anderen Vertices nennt man reguläre Vertizes.

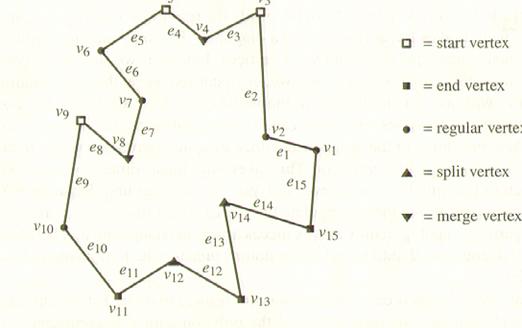
Im Falle p_y = q_y werden die Vertizes im Uhrzeigersinn abgelaufen

(der Vertex mit dem kleineren x - Wert kommt zuerst).

Um ein monotones Polygon zu bekommen, müssen wir die Merge- und Split-Vertices beseitigen.

Dies geschieht durch das Ziehen von Diagonalen zu anderen Vertizes des entsprechenden Polygons.

Bei Split-Vertizes geht man folgendermaßen vor:

Eine imaginäre Linie l wird solange von unten nach oben bewegt, bis sie auf einen Vertex trifft.

Wenn sich der Vertex oberhalb des Split-Vertex befindet und die Verbindungslinie zwischen dem Split-Vertex und dem Ziel-Vertex im Polygon liegt, dann entsteht eine neue Kante und das Polygon wird geteilt.

Sonst wird die Linie zum nächst oberhalb liegenden Vertex bewegt.

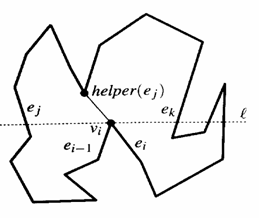
Im Falle eines Merge-Vertex wird die Linie l von oben nach unten bewegt. Der erste unterhalb liegende Vertex, bei dem die Verbindungslinie mit dem Merge-Vertex im Polygon liegen würde, wird mit diesem verbunden.

Nach dem ersten Schritt bekommt man folgendes Bild.

Nun ist die Zerlegung in monotone Regionen abgeschlossen und wir wenden uns der eigentlichen Dreieckszerlegung zu.

1.4.1 Dreieckszerlegung monotoner Polygone

Sei P ein y - monotones Polygon mit n Vertizes. Die n Vertizes werden nach ihren y-Werten sortiert.

Dann bewegt man sich vom obersten Vertex zum untersten.

Wenn zwei Vertizes den gleichen y-Wert haben, so behandelt man den mit dem kleineren x - Wert zuerst (Im Uhrzeigersinn).

Der Algorithmus verarbeitet die sortierten Vertizes der Reihe nach, beginnend mit dem Vertex mit dem grössten y-Wert. Es wird ein Keller S angelegt, auf welchen diejenigen Vertizes gelegt werden, zu denen noch Diagonalen hinzugefügt werden können. Wenn man einen Vertex bearbeitet, zieht man so viele Diagonalen wie möglich zu den Vertizes, die sich noch auf dem Keller befinden, wobei die Diagonalen im Polygon liegen müssen. Vom letzten Vertex mit dem kleinsten y-Wert aus wird versucht, Diagonalen zu allen anderen Vertizes außer dem ersten und letzten zu ziehen.

Der Algorithmus hat folgende Struktur:

Die sortierten Vertizes werden in einer doppeltverketteten Liste D gelagert.

Seien u₁ ,u₂, ...,u_n die sortierten Vertizes.

Man initialisiert einen leeren Keller S und u₁ ,u₂, ...,u_n werden auf den Keller gepackt.

for j <= 3 to n - 1

do if

u_j und der Vertex oben auf S auf verschiedenen Kanten liegen

then

alle Vertizes werden von S gepopt, Setzen einer Diagonale in D von u_j zu jedem gepopten Vertex außer dem letzten.

u_{j - 1} und u_j werden auf S gepusht.

else

ein Vertex wird von S gepopt. Die anderen Vertizes aus S werden gepopt, solange die Diagonalen in D sind.

Der letzte Vertex der gepopt worden ist, wird wieder auf S gepusht. u_j wird auf S gepusht.

Diagonalen von u_n zu allen Vertizes auf S außer dem ersten und letzten ziehen.

2.0 Shading Problems

Es gibt Fälle, in welchen eine einfache Tesselierung nicht zu einem akzeptablen Ergebnis führt.

Man muss dann bei der Tesselierung einige Dinge berücksichtigen. Manchmal sind z.B. auf Polygonen Netze aufgespannt (um Bowtie-Vierecke zu vermeiden). Dabei stellt sich die Frage, welches der beste Weg ist, die durch das Netz entstehenden Vierecke in Dreiecke zu zerlegen.

Es gibt verschiedene Ansätze, abhängig von gewünschten Effekten:

Für Vierecke ohne zusätzliche Informationen ist es das Beste, die kürzere der beiden Diagonalen für die Zerlegung zu verwenden.

Für Vierecke mit unterschiedlichen Farbwerten pro Vertex ist es besser, die Vertices mit dem kleinsten Farbwertunterschied zu verbinden.

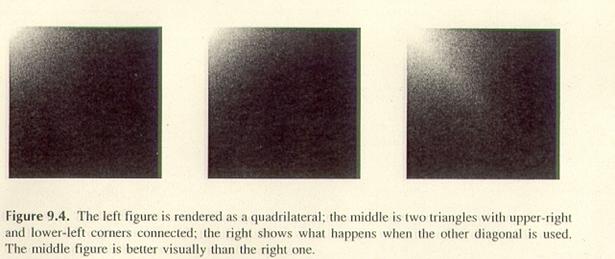
Unten sieht man drei mal das gleiche Viereck. Das linke Bild zeigt das ursprüngliche, das mittlere das korrekt tesselierte und das rechte Bild das unakzeptabel tesselierte Viereck.

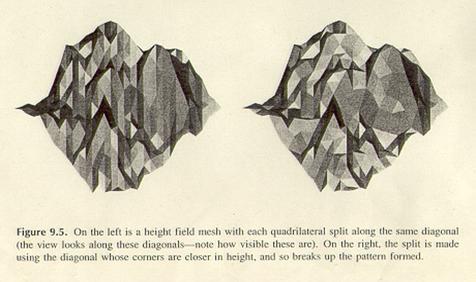
Auch bei Landschaften kann es zu einem nicht akzeptablen Ergebnis bei der Tesselierung kommen. Hier gibt es mehrere Möglichkeiten, dieses zu vermeiden. Zum Beispiel:

- diejenige Diagonale zu nehmen, welche zwei gleich große Dreiecke produziert.

- Verbinden der Vertices mit dem kleinsten oder größten Höhenunterschied. (Verfahren I)

Links ist immer die gleiche Diagonale verwendet worden, rechts Verfahren I.

Es gibt Fälle, in welchen Dreiecke das Innere von Vierecken nicht richtig darstellen können.

Ein Weg dieses zu verbessern, ist ein Netz aufzuspannen, andere Texturinterpolationsschemata zu wählen oder aber Gouard Shading auf das ganze Viereck anzuwenden.

3.0 Edge Cracking

Einige Modelers benutzen NURBS (Non-Uniform Rational B-Splines) um Kurven zu beschreiben .

Über die Splineflächen sind meistens Netze aufgespannt, um sie leichter rendern zu können.

Vorgehensweise:

Man geht schrittweise über die Spline Kurve, definiert die Fläche und berechnet den Vertex und die zugehörige Diagonale.

Ein Problem kann entstehen, wenn sich zwei Splineflächen treffen und die Punkte auf der gemeinsamen Kante nicht für beide Flächen gleich sind. Das linke Bild zeigt wie sogenannte Cracks entstehen können, wenn sich die Splineflächen treffen, das mittlere das korrigierte Bild und das rechte das korrekte Bild ohne der Entstehung von Cracks.

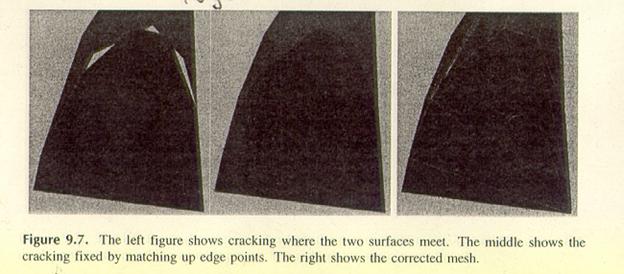
Edge Stitching nennt man den Prozess um dieses Problem zu korrigieren. Dabei muss man sicherstellen, dass alle Punkte für beide Splineflächen gleich sind.

4.0 T-Vertices

Dieses Problem entsteht, wenn zwei benachbarte Flächen versuchen, die Vertizes an der gemeinsamen Kante zu teilen. Die benachbarten Flächen können verschiedene Vertizes an der gemeinsamen Kante haben. Dabei entsteht eine so genannte T- intersection .

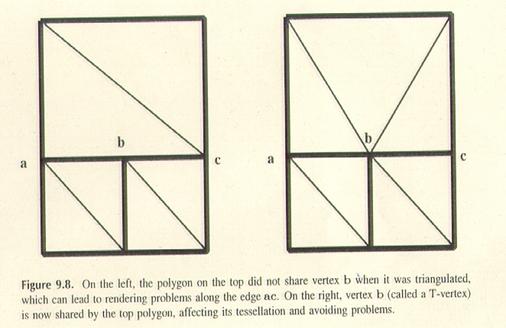
Dieses Problem kann total eliminiert werden, wenn man solche Kanten sucht (meistens eine sehr schwierige Prozedur) und sicherstellt, dass die Vertizes von allen angrenzenden Flächen geteilt werden.

Wie man eine T-intersection vermeiden kann, ist gut beschrieben im Artikel von Cignoni, P., C. Montani, and R. Scopigno, "Triangulating Convex Polygons Having T-Vertices," journal of graphics tools, vol. 1, no. 2, pp. 1-4, 1996.

Literature:

1. Real-Time Rendering, by Tomas Akenine-Möller and Eric Haines, ~880 pages, from A.K. Peters Ltd., 2nd edition

2. Computational geometry : algorithms and applications / Mark de Berg; Marc van Krefeld….-2nd, rev.ed

Websites: www.opengl.org, flipcode.com, fly.srk.fer.hr, www.fh-landshut.de